UVa 1394 - And Then There Was One

#思维 #递推 #DP #约瑟夫问题

Published on 2016-02-04

描述

有 $n(n\le10000)$ 个人顺时针排成一个圆圈，依次顺时针标号 $1 - n$ 。一开始标号为 $m$ 的退出，剩下的人从 $1$ 开始，每隔 $k(k\le10000)$ 个人退出一个，问最后一个退出的人是谁？

样例输入

8 5 3
100 9999 98
10000 10000 10000
0 0 0

样例输出

1
93 2019

分析

我想尽量使用清晰易懂的语言来阐述这道题，先看普通的约瑟夫问题。在这之前，我们有必要理解间隔 $k$ 个人杀人是什么意思。
这是间隔 $2$ 个人杀人，可以看到，第一个杀死的人是 $k - 1$ 号！

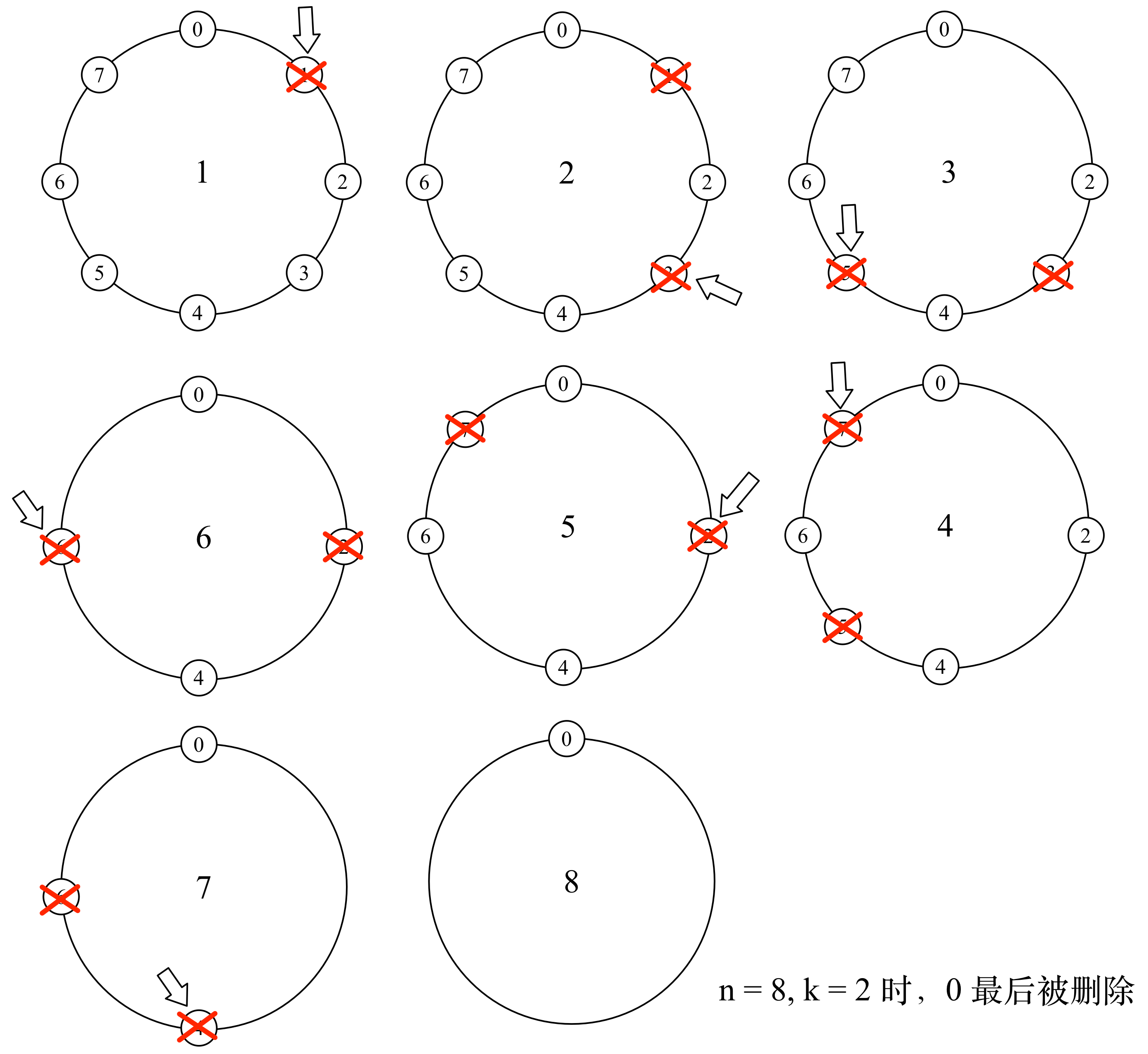
由于我们只关心最后一个被删除的人，并不关心最后的过程，所以，我们没有必要也不能够模拟整个过程。我们用递推解决。假设有 $n$ 个人围成环，标号为 $[0, n - 1]$ （从 $0$ 开始的好处是取模方便），每数 $k$ 个人杀一个的情况下，最后一个存活的人的编号是 $f[n]$ 。
我们有 $f[1] = 0$ ，这不需要解释。
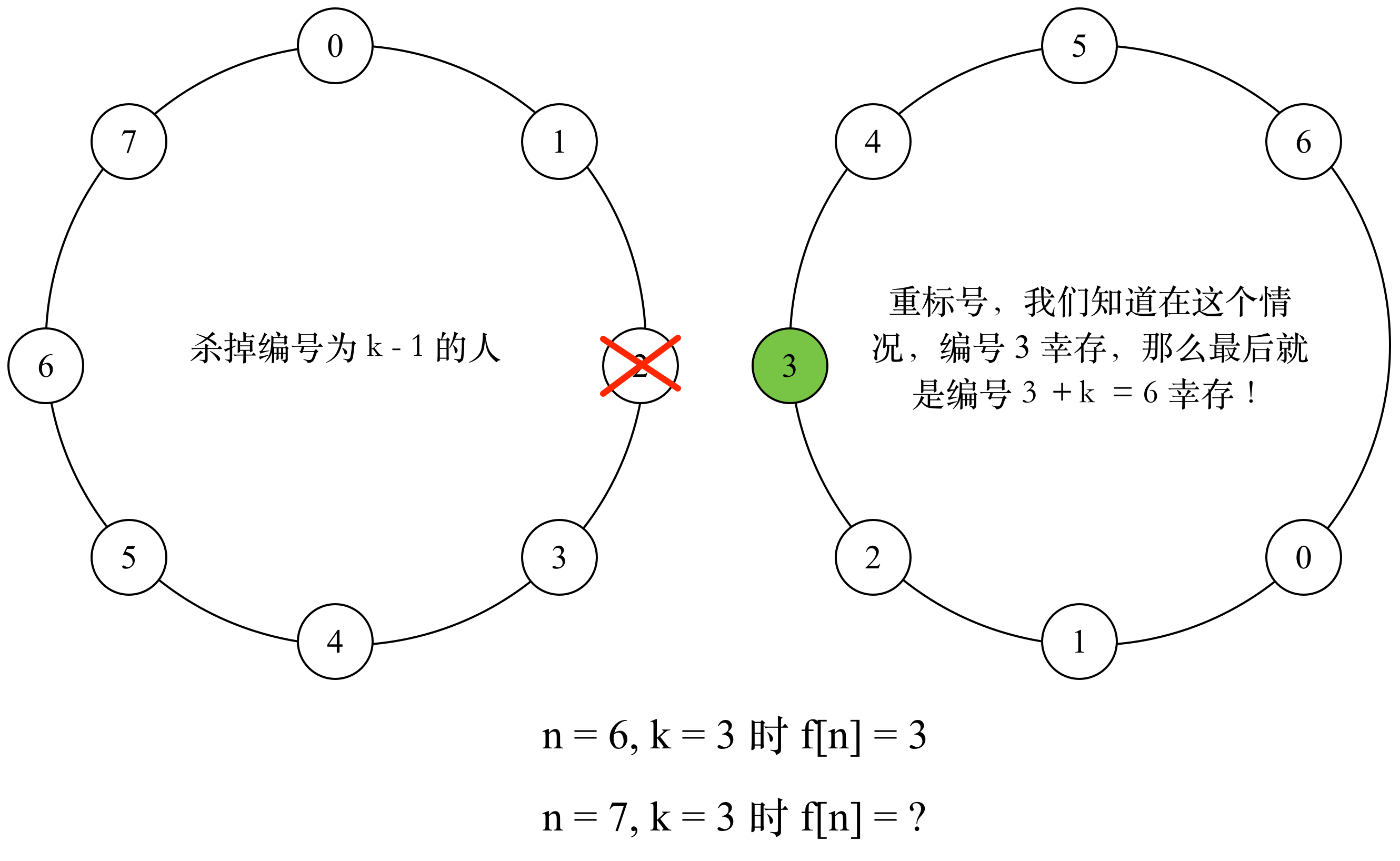
接着考虑一般情况 $f[n]$ ，第一个杀死的人的编号是 $k - 1$ ，杀死后只剩下 $n - 1$ 个人了，那么我们重新编号！
原来编号为 $k$ 的现在是 $0$ 号，也就是编号之间相差 $3$ ，我们只要知道现在 $n - 1$ 个人的情况最后是谁幸存，也就知道 $n$ 个人是谁幸存。幸运的是 $f[n - 1]$ 已经算出来了，那 $f[n]$ 就是在 $f[n - 1]$ 的基础上加上一个 $k$ 即可，不要忘记总是要取模。
所以递推式子是：

那么本题就简单了，假设标号还是从 $0$ 开始，那么原先要第一个要杀的人是编号为 $k - 1$ 的，现在第一个要杀的编号是 $m - 1$ ，还是重标号，答案是 $f[n] + m - k$ 。取模，以及变正后（取模也可能有负数）为：

由于题目中编号从 $1$ 开始，最终答案：

给张图看看先删除编号为 $m - 1$ 的人的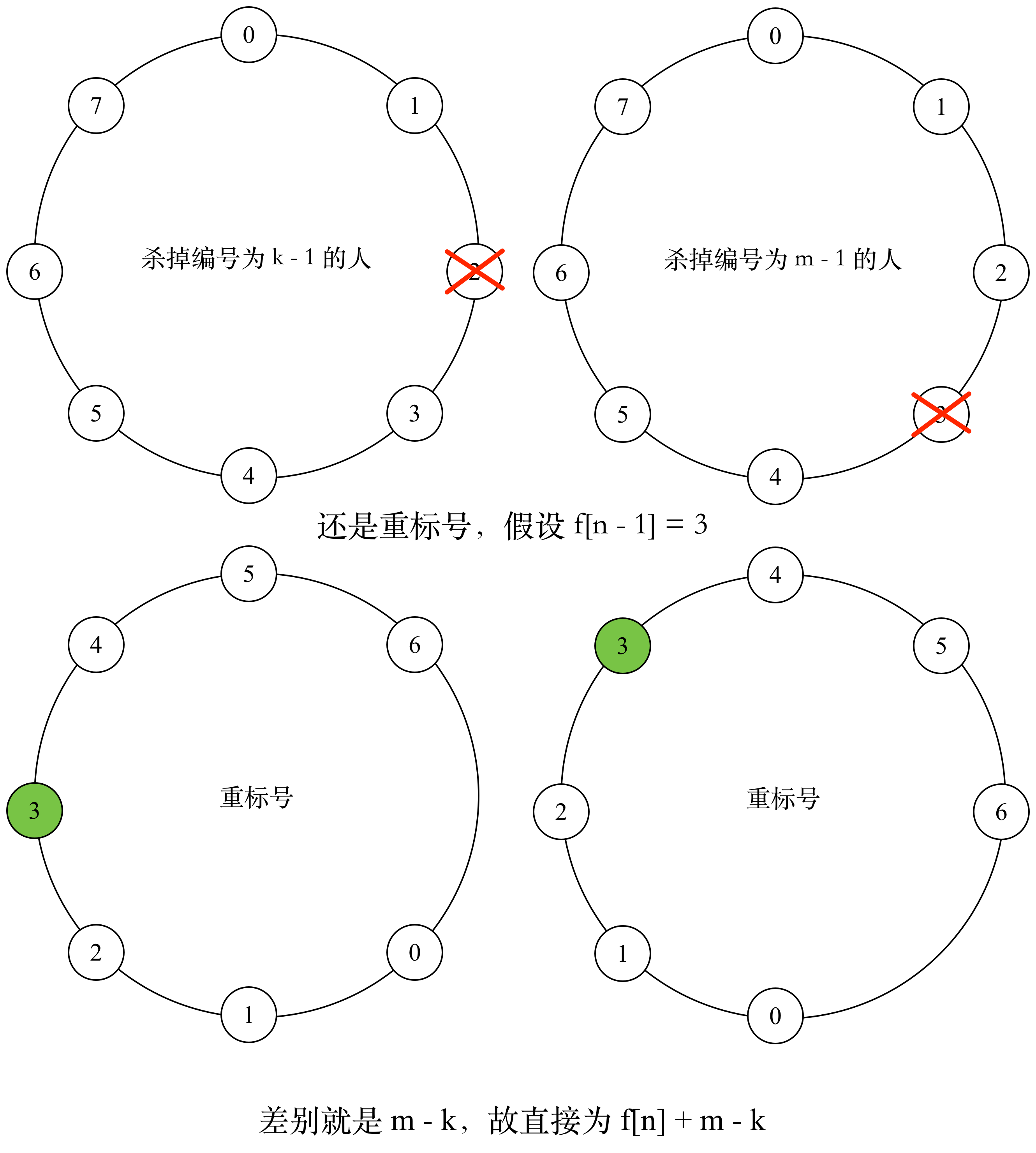影响：

代码

直观一点的：

//  Created by Sengxian on 2/4/16.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  UVa 1394 约瑟夫问题变形（递推）
#include <algorithm>
#include <iostream>
#include <cctype>
#include <climits>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <vector>
#include <stack>
#include <queue>
#define br putchar('\n');
using namespace std;

inline int ReadInt() {
    int n = 0, ch = getchar();
    while(!isdigit(ch)) ch = getchar();
    while(isdigit(ch)) n = n * 10 + ch - '0', ch = getchar();
    return n;
}

const int maxn = 10000 + 3;
int n, m, k, f[maxn];

inline int mod(const int x) {
    return ((x % n) + n) % n;
}
int main() {
    while(n = ReadInt(), k = ReadInt(), m = ReadInt(), n + m + k) {
        f[1] = 0;
        for(int i = 2; i <= n; ++i)
            f[i] = (f[i - 1] + k) % i;
        printf("%d\n", mod(f[n] + m - k) + 1);
    }
    return 0;
}

优化掉数组：

//  Created by Sengxian on 2/4/16.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  UVa 1394 约瑟夫问题变形（递推）
#include <algorithm>
#include <iostream>
#include <cctype>
#include <climits>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <vector>
#include <stack>
#include <queue>
#define br putchar('\n');
using namespace std;

inline int ReadInt() {
    int n = 0, ch = getchar();
    while(!isdigit(ch)) ch = getchar();
    while(isdigit(ch)) n = n * 10 + ch - '0', ch = getchar();
    return n;
}

int n, m, k;

inline int mod(const int x) {
    return ((x % n) + n) % n;
}
int main() {
    while(n = ReadInt(), k = ReadInt(), m = ReadInt(), n + m + k) {
        int tmp = 0;
        for(int i = 2; i <= n; ++i)
             tmp = (tmp + k) % i;
        printf("%d\n", mod(tmp + m - k) + 1);
    }
    return 0;
}

附加输入

附加输出

Dynamic Programming Exercises Beginner 归档题解(1) UVa 1312 - Cricket Field

Sengxian's Blog