边－双联通分量四题

Published on 2015-12-16

几道题折磨了我半天，看来还是太弱。。。。发一下这种添加边类型的题的题解吧。
注：读之前请确保已经理解了无向图双联通分量的 tarjan 算法，我这里是训练指南的版本。

POJ 3352 - Road Construction

题目地址
现有一个连通的无向图，共有 $n(3\le n\le1000)$ 个节点， $m(2\le m\le1000)$ 条无向边，求至少需要添加多少条无向条边，使得任意删除一条边，图仍然连通的？

分析

题意比较清楚，任意删去一条边，图仍然联通，意味着任意两点之间至少有有两条不重叠的路径连接，这正是边－双联通分量（Biconneted Component）的特性。
现在题目是要求添加最少的边，使得图边－双联通，怎么处理呢？
首先想到缩点，即首先计算出所有边－双联通分量，由于边－双联通分量内部一定满足删除一条边，仍然联通，所以可以把它们看作一个“点”。我们要做的，正是让这些“点”满足边－双联通，这样就可以保证任意两点之间满足边－双联通。
慢慢来，首先怎么计算边－双联通分量呢？一个可行的方案是首先标记出所有的桥，然后再对全图进行dfs（不走桥），每一次dfs都意味着有一个新的边－双联通分量。如图所示，我们得到了缩点后得到的图，这个图肯定是没有环的，否则就可以合并，它是一棵树。

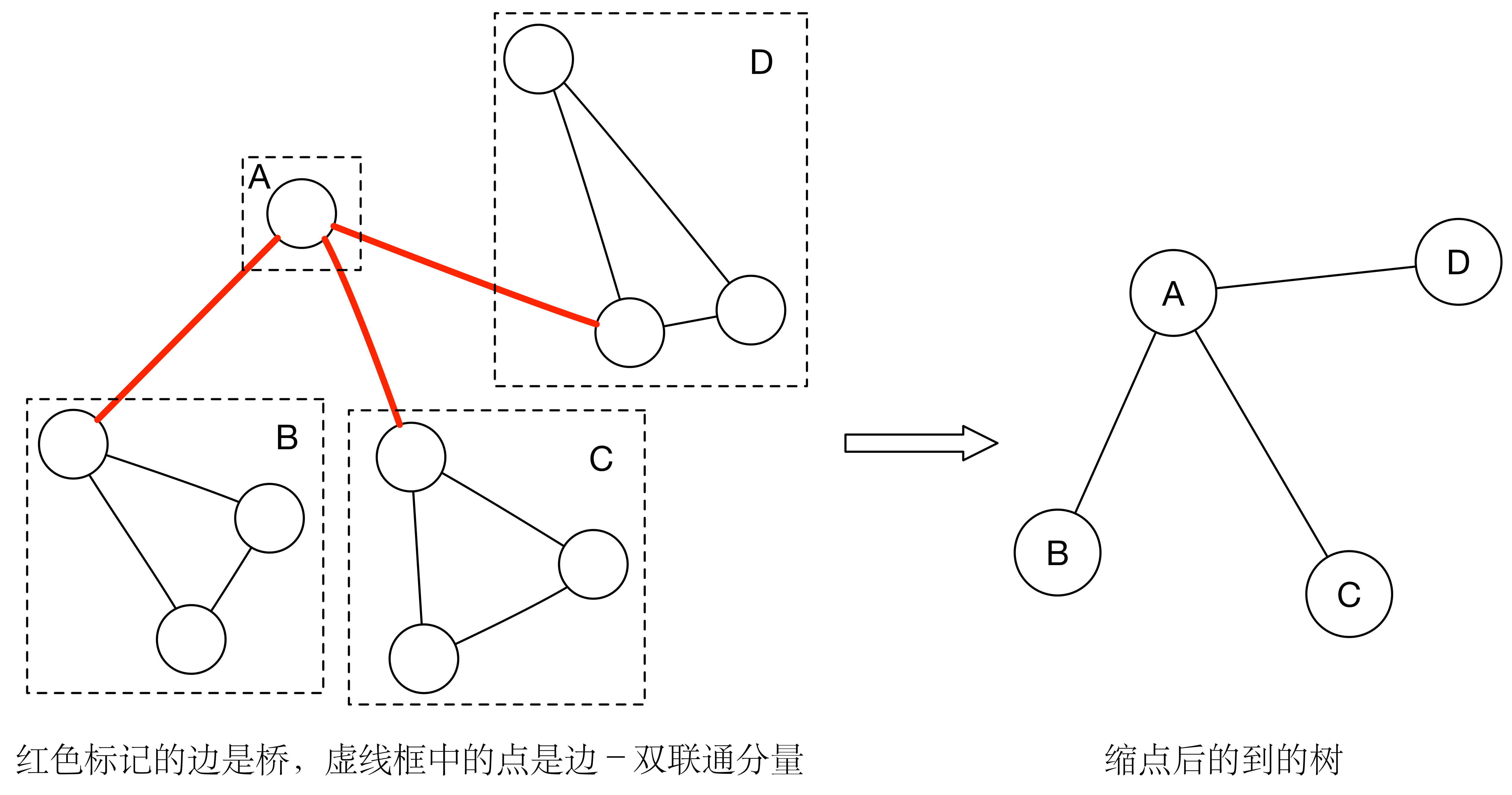
接下来的工作，就是要用最少的边，使得新图双联通，怎么办呢？如果得到的树的叶子数量是 $leaf$ （度为1的节点），答案就是 $\left\lceil\frac{leaf}{2} \right\rceil$ 。怎么严谨证明呢（网上几乎没有证明）？考虑贪心算法。

引理一：在联通图缩点后得的一棵树中，若叶子节点的数量是 $leaf$ ，则在原图中至少需要添加 $\left\lceil\frac{leaf}{2} \right\rceil$ 条边，才能使全图边－双联通。
证明： 如果我们每步都将尽可能多的点消去，那么到了最后，我们一定能用最少的步数使全图边－双联通。
考虑将叶子节点进行配对，两叶子节点之间连一条边就可以形成一个圈，所以我们每次找到树的直径（即距离最远的两个叶子节点），在两点之间连一条边，这样这个当前能形成的最大的圈（圈满足边－双联通）就可以缩为一个点，这样就保证了每次消去了尽可能多的点。反复进行此操作，每步消去两个叶子节点，若 $leaf$ 为偶数，则正好需要 $\frac{leaf}{2}$ 步。如果是奇数，则最后一定剩下两个点，在两个点之间连接一条边形成圈，最后剩余一个点，需要 $\frac{leaf + 1}{2}$ 步。综合起来总共需要 $\left\lceil\frac{leaf}{2} \right\rceil$ 步。

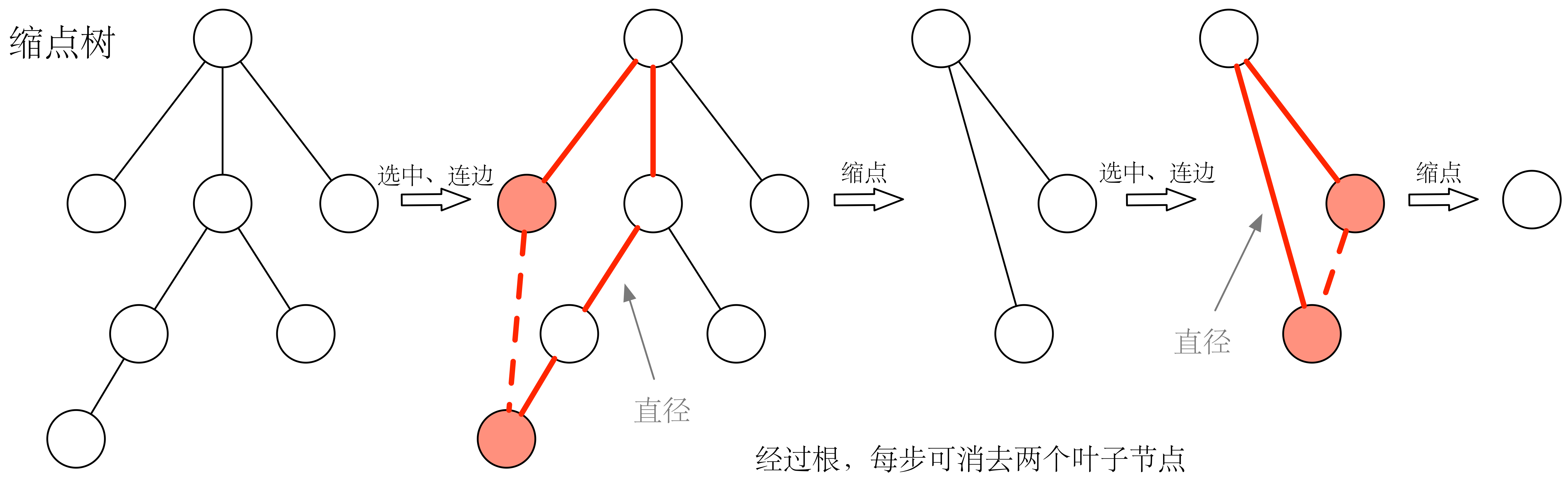
有趣的是，我们每次找的两个叶子节点并不需要一定是树的直径两个端点，只要满足他们的 $LCA$ （最近公共祖先，Least Common Ancestors）是树根就行了，这样就一定可以保证每次消去两个叶子节点（实质上是可以看作缩为树根）。
接着反证法，如果每次找的两个叶子节点的 $LCA$ 不是树根，那么这两个点之间连一条边只会形成一个包括他们的 $LCA$ 的圈，消去后这个 $LCA$ 还是叶子节点，所以只能减少一个叶子节点，由于最终的目的是缩成一个点。所以需要的步数一定比之前的方法多，所以矛盾。
为了加深理解，还是放图。

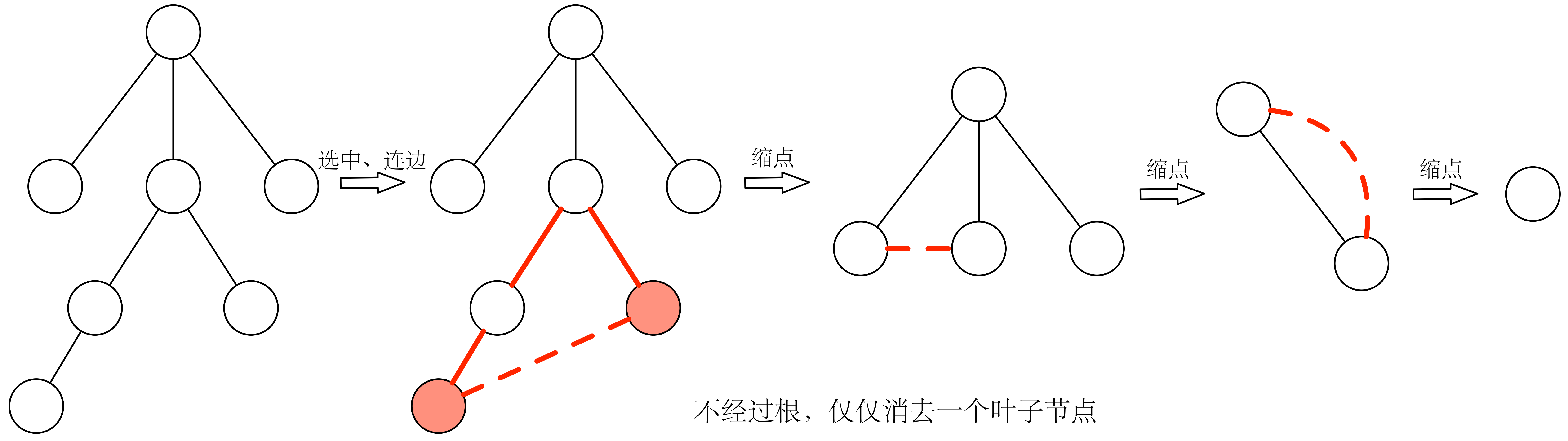
注意，上面的缩点树都是默认以树的重心为根的，为了避免退化（无法找到两点的 $LCP$ 为树根）。事实上，第一次找到重心以后，每次找直径，之后都可以以圈缩成的那个点为重心。
那么，算法已经清晰了，剩下就是能不能写对的问题了（不写熟就有各种奇葩错误。。。

代码

//  Created by Sengxian on 12/16/15.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  Poj 3352 边-双连通
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <vector>
#include <stack>
using namespace std;
const int maxn = 1000 + 3;
struct edge {
    int to, iscut, rev;
    edge(int to, int iscut, int rev): to(to), iscut(iscut), rev(rev) {}
};
vector<edge> G[maxn];
int n, m, degree[maxn], bccno[maxn], pre[maxn], bcc_cnt, timestamp;

int dfs(int cur, int fa) {
    int lowu = pre[cur] = ++timestamp;
    for(int i = 0; i < G[cur].size(); ++i) {
        edge &e = G[cur][i];
        int v = e.to;
        if(!pre[v]) {
            int lowv = dfs(v, cur);
            lowu = min(lowu, lowv);
            if(lowv > pre[cur]) e.iscut = true, G[e.to][e.rev].iscut = true;
        }else if(pre[v] < pre[cur] && v != fa)
            lowu = min(lowu, pre[v]); //反向边，注意到父亲的不是反向边
    }
    return lowu;
}

bool vis[maxn];
void dfs1(int u) {
    vis[u] = true;
    bccno[u] = bcc_cnt;
    for(int i = 0; i < G[u].size(); ++i) {
        edge e = G[u][i];
        if(e.iscut) continue;
        if(!vis[e.to]) dfs1(e.to);
    }
}

void find_bcc() {
    memset(bccno, 0, sizeof(bccno));
    memset(pre, 0, sizeof(pre));
    memset(vis, 0, sizeof(vis));
    timestamp = bcc_cnt = 0;
    for(int i = 0; i < n; ++i) 
        if(!pre[i]) dfs(i, -1); //第一次dfs求出所有的桥
    for(int i = 0; i < n; ++i) //在全图dfs一次，找出每个边－双联通分量
        if(!vis[i]) bcc_cnt++, dfs1(i);
}

void Solve() {
    find_bcc();
    for(int u = 0; u < n; ++u)
        for(int i = 0; i < G[u].size(); ++i) {
            int v = G[u][i].to;
            if(G[u][i].iscut) degree[bccno[v]]++; //桥对应缩点树中的边，统计入度
        }
    int cnt = 0;
    for(int i = 1; i <= bcc_cnt; ++i)
        if(degree[i] == 1) cnt++;
    printf("%d\n", (cnt + 1) / 2);
}

inline int ReadInt() {
    int n = 0, ch = getchar();
    while(ch < '0' || ch > '9') ch = getchar();
    do {
        n = n * 10 + ch - '0';
        ch = getchar();
    }while(ch >= '0' && ch <= '9');
    return n;
}

int main() {
    //freopen("test.in", "r", stdin);
    n = ReadInt(), m = ReadInt();
    for(int i = 0; i < m; ++i) {
        int f = ReadInt() - 1, t = ReadInt() - 1;
        G[f].push_back(edge(t, 0, G[t].size()));
        G[t].push_back(edge(f, 0, G[f].size() - 1));
    }
    Solve();
    return 0;
}

POJ 3177 - Redundant Paths

题目地址
有 $n(1\le n\le5000)$ 个牧场，它们之间是联通的，Bessie 要从一个牧场到另一个牧场，要求至少要有 2 条独立的路可以走。现已有 $m(1\le m\le10000)$ 条路，求至少要新建多少条路，使得任何两个牧场之间至少有两条独立的路。两条独立的路是指：没有公共边的路，但可以经过同一个中间顶点。

分析

几乎与上面的题一模一样，不过此题有重边，注意两条重边只算一条，即 $u\rightarrow v$ 之多只有一条路，很好处理，unique 一下即可。

代码

//  Created by Sengxian on 12/16/15.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  Poj 3177 边-双连通 注意重边
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <vector>
#include <stack>
using namespace std;
const int maxn = 5000 + 3;
struct edge {
    int to, iscut, rev;
    bool operator < (const edge &e) const {
        return to < e.to;
    }
    bool operator == (const edge &e) const {
        return to == e.to;
    }
    edge(int to, int iscut, int rev): to(to), iscut(iscut), rev(rev) {}
};
vector<edge> G[maxn];
int n, m, degree[maxn], bccno[maxn], pre[maxn], bcc_cnt, timestamp;

int dfs(int cur, int fa) {
    int lowu = pre[cur] = ++timestamp;
    for(int i = 0; i < G[cur].size(); ++i) {
        edge &e = G[cur][i];
        int v = e.to;
        if(!pre[v]) {
            int lowv = dfs(v, cur);
            lowu = min(lowu, lowv);
            if(lowv > pre[cur]) e.iscut = true, G[e.to][e.rev].iscut = true;
        }else if(pre[v] < pre[cur] && v != fa)
            lowu = min(lowu, pre[v]); //反向边，注意到父亲的不是反向边
    }
    return lowu;
}

bool vis[maxn];
void dfs1(int u) {
    vis[u] = true;
    bccno[u] = bcc_cnt;
    for(int i = 0; i < G[u].size(); ++i) {
        edge e = G[u][i];
        if(e.iscut) continue;
        if(!vis[e.to]) dfs1(e.to);
    }
}

void find_bcc() {
    memset(bccno, 0, sizeof(bccno));
    memset(pre, 0, sizeof(pre));
    memset(vis, 0, sizeof(vis));
    timestamp = bcc_cnt = 0;
    for(int i = 0; i < n; ++i)
        if(!pre[i]) dfs(i, -1);
    for(int i = 0; i < n; ++i)
        if(!vis[i]) bcc_cnt++, dfs1(i);
}

void Solve() {
    find_bcc();
    for(int u = 0; u < n; ++u) {
        for(int i = 0; i < G[u].size(); ++i) {
            int v = G[u][i].to;
            if(G[u][i].iscut) degree[bccno[v]]++;
        }
    }
    int cnt = 0;
    for(int i = 1; i <= bcc_cnt; ++i)
        if(degree[i] == 1) cnt++;
    printf("%d\n", (cnt + 1) / 2);
}

inline int ReadInt() {
    int n = 0, ch = getchar();
    while(ch < '0' || ch > '9') ch = getchar();
    do {
        n = n * 10 + ch - '0';
        ch = getchar();
    }while(ch >= '0' && ch <= '9');
    return n;
}

int main() {
    n = ReadInt(), m = ReadInt();
    for(int i = 0; i < m; ++i) {
        int f = ReadInt() - 1, t = ReadInt() - 1;
        G[f].push_back(edge(t, 0, G[t].size()));
        G[t].push_back(edge(f, 0, G[f].size() - 1));
    }
    for(int i = 0; i < n; ++i) {
        G[i].erase(unique(G[i].begin(), G[i].end()), G[i].end());
    }
    Solve();
    return 0;
}

UVa 610 - Street Directions

题目地址
之前发过了，大家直接去看看就好了，为了保证完整，我还是搬过来。
http://blog.sengxian.com/solutions/uva-610
有 $n(n\le1000)$ 个节点，另有 $m$ 条双向道路。任务是将尽可能多的道路改造成单向道路，使得改造后的图仍然联通（每个节点相互可达）。

分析

初始的图是无向图，那么 $u\rightarrow v$ 至少得有两条不重叠的道路，才可以使改成无向边之后 $u\rightarrow v,v\rightarrow u$ 至少有一条路径。那么算法已经清晰了，对无向图求边-双连通分量，找出桥所有的桥即可。所有的桥必须是双向道路，其余的都可以改造成单向道路。
打印顺序是任意的，我们先用dfs顺着打印路径，不走重边（包括反边），不走桥，用类似欧拉回路的方法不停地找环。这样就可以将原先每个边-双连通分量内部所有点强连通，最后打出所有桥，使得全图强连通。

代码

//  Created by Sengxian on 12/15/15.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  UVa 610 双连通+割边
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <vector>
#include <stack>
using namespace std;
const int maxn = 1000 + 3;
struct edge {
    int to, iscut, rev, used;
    edge(int to, int iscut, int rev, int used): to(to), iscut(iscut), rev(rev), used(used) {}
    edge() {}
};
vector<edge> G[maxn];
vector<pair<int, int> > cuts;
int n, m, pre[maxn], timestamp;
bool vis[maxn];

int dfs(int u, int fa) {
    int lowu = pre[u] = ++timestamp;
    for(int i = 0; i < G[u].size(); ++i) {
        edge &e = G[u][i];
        int v = e.to;
        if(!pre[v]) {
            int lowv = dfs(v, u);
            lowu = min(lowu, lowv);
            if(lowv > pre[u]) {
                e.iscut = true;
                G[e.to][e.rev].iscut = true;
                cuts.push_back(make_pair(u, v));
            }
        }else if(pre[v] < pre[u] && v != fa) lowu = min(lowu, pre[v]);
    }
    return lowu;
}

void find_bcc() {
    cuts.clear();
    memset(pre, 0, sizeof(pre));
    timestamp = 0;
    for(int i = 0; i < n; ++i)
        if(!pre[i]) dfs(i, 0);
}

void print(int x) {
    vis[x] = true;
    for(int i = 0; i < G[x].size(); ++i) {
        edge &e = G[x][i];
        if(e.iscut || e.used) continue;
        e.used = true;
        G[e.to][e.rev].used = true;
        printf("%d %d\n", x + 1, e.to + 1);
        if(!vis[e.to]) print(e.to); //不走重复路！
    }
}

inline int ReadInt() {
    int n = 0, ch = getchar();
    while(ch < '0' || ch > '9') ch = getchar();
    do {
        n = n * 10 + ch - '0';
        ch = getchar();
    }while(ch >= '0' && ch <= '9');
    return n;
}

int main() {
    int caseNum = 0, f, t;
    while(n = ReadInt(), m = ReadInt()) {
        for(int i = 0; i < n; ++i) G[i].clear();
        printf("%d\n\n", ++caseNum);
        for(int i = 0; i < m; ++i) {
            f = ReadInt() - 1, t = ReadInt() - 1;
            G[f].push_back(edge(t, 0, G[t].size(), 0));
            G[t].push_back(edge(f, 0, G[f].size() - 1, 0));
        }
        find_bcc();
        memset(vis, 0, sizeof(vis));
        for(int i = 0; i < n; ++i)
            if(!vis[i]) print(i);
        //割边必须双向，否则图不能连通
        for(int i = 0; i < cuts.size(); ++i)
            printf("%d %d\n%d %d\n", cuts[i].first + 1, cuts[i].second + 1, cuts[i].second + 1, cuts[i].first + 1);
        printf("# \n");
    }
}

UVa 10972 - RevolC FaeLoN

题目地址
给定一个 $n(1\le n\le1000)$ 个顶点的无向图，要求将所有边变为有向边，求最少加入多少条有向边，使得该图强连通？

分析

首先要绕过弯来，变成有向图强联通，不就是无向图双联通嘛，所以题目成功转化为了上面的模型。
等等，我怎么WA了，太天真了。。。这题没说是联通图啊，所以缩点得到的不一定是树了，有可能是森林，之前的计算公式已经不适用了，不过可以简单的推一下。
首先对于每棵树内部，根据引理一，计算结果为 $\left\lceil\frac{leaf}{2} \right\rceil$ ，所以让所有的树双联通的边数量是 $\left\lceil\frac{\sum\limits_{t\in trees}leaf(t)}{2} \right\rceil$ ，统计所有度为 1 的点就行了。剩下孤立的点没有考虑，每个孤立的点最少向其他树连两条边就可以让这个点参与进来。
有的同学就会疑惑了，抛开孤立点不谈，对每棵树而言，统计度为 1 的点只能让自己这一棵树双联通啊，怎么能保证整个森林联通呢？比如下面这组数据（答案是2），以及缩点后的图：

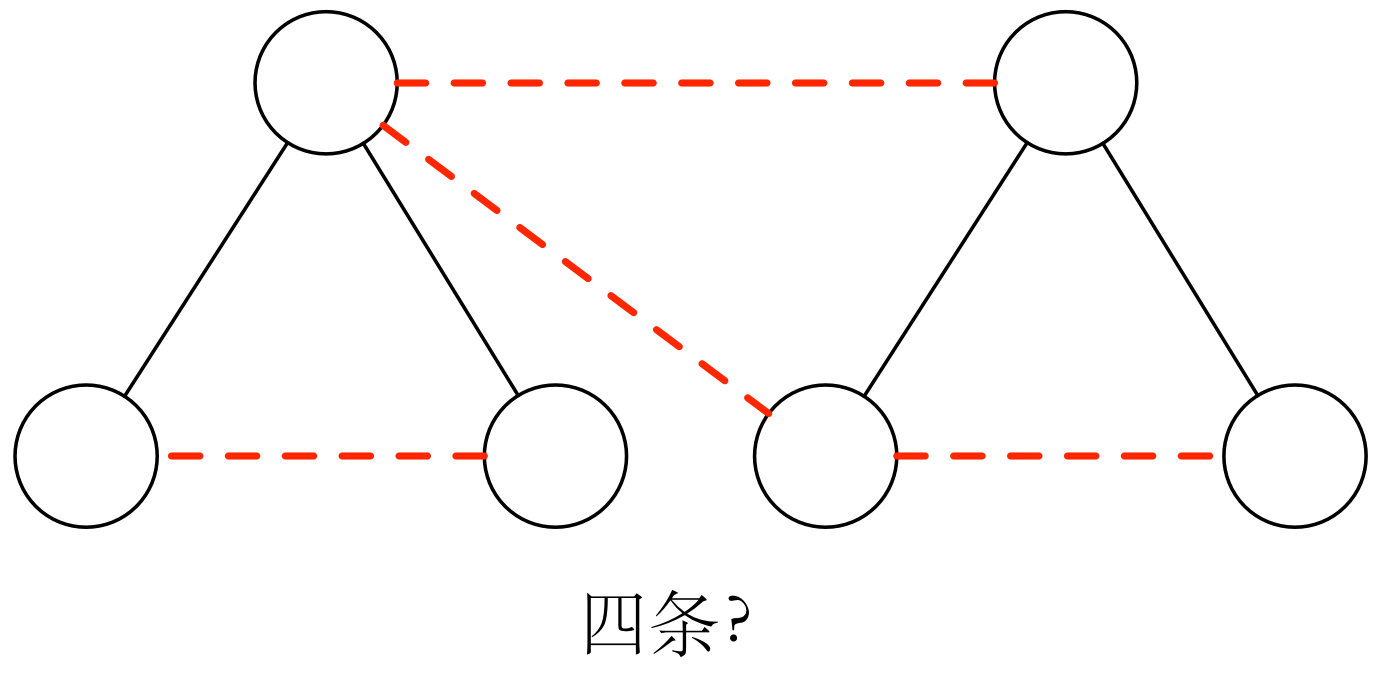
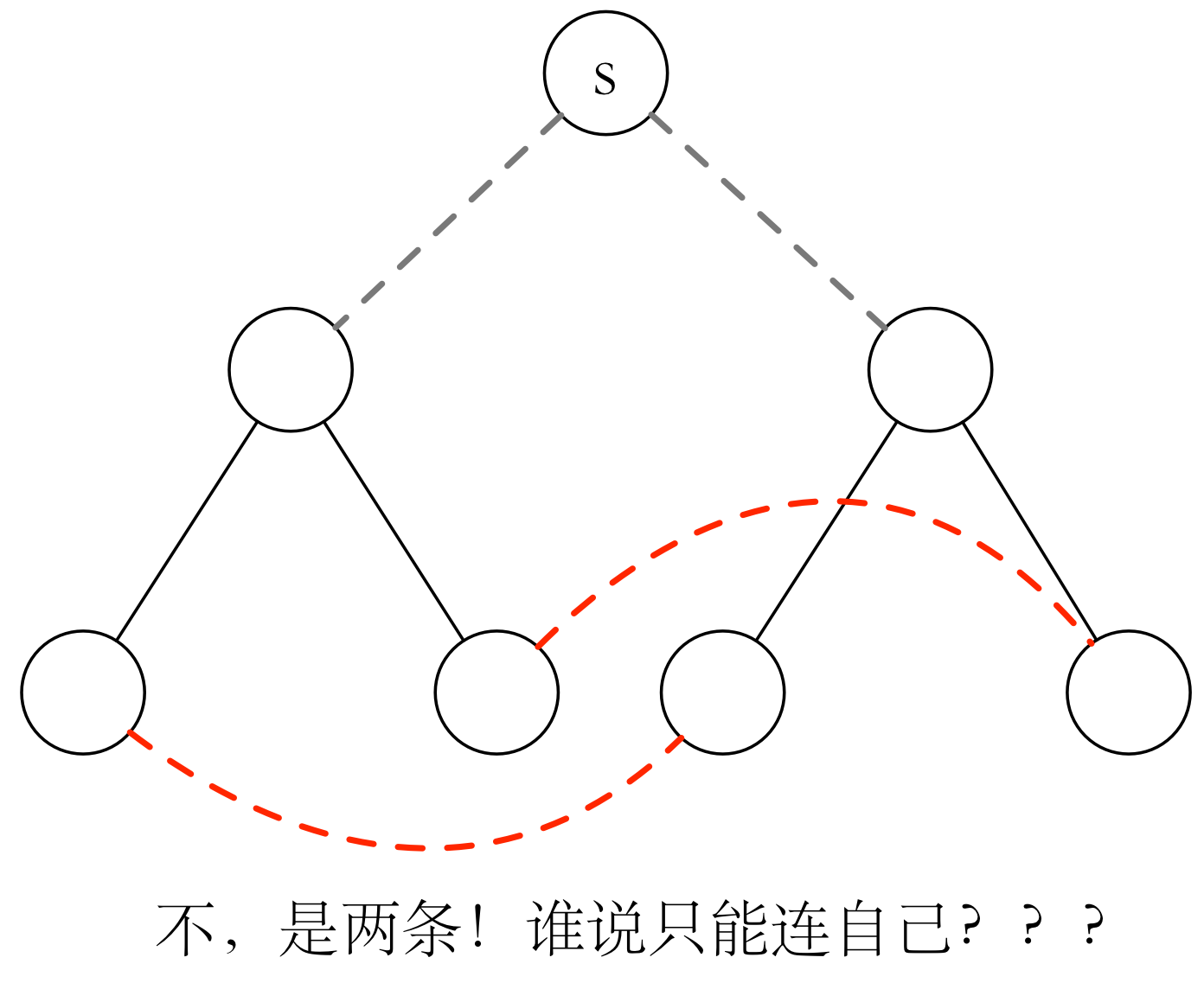
哈哈哈，算漏了吧，加一个超级根就行了，不一定非要连自己树上的点啊，显然，每次连接选择不同树上的点更优。总之，对于不是联通的森林来说，加一个超级根，保证每次选择的叶子节点的LCA是超级根，就可以得到最优的结果。
这样，可以使用一个 $cnt$ 变量计数，遇到度为 1 的点就 +1，度为 0 的点 +2，最后答案就是 $\left\lceil\frac{cnt}{2}\right\rceil$ 。比较容易WA的点是如果原图边－双连通，我们的算法会把唯一的一个点算作孤立点，故特判 $\mathrm{bcc\_cnt} = 1$ 时答案为 0 即可。

代码

//  Created by Sengxian on 12/16/15.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  UVa 10972 边双连通
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
using namespace std;
const int maxn = 1000 + 3;
struct edge {
    int to, iscut, rev;
    edge(int to, int iscut, int rev): to(to), iscut(iscut), rev(rev) {}
};
vector<edge> G[maxn];
int n, m, pre[maxn], bccno[maxn], degree[maxn], timestamp, bcc_cnt, block_cnt;

int dfs(int u, int fa) {
    int lowu = pre[u] = ++timestamp;
    for(int i = 0; i < G[u].size(); ++i) {
        edge &e = G[u][i];
        int v = e.to;
        if(!pre[v]) {
            int lowv = dfs(v, u);
            lowu = min(lowv, lowu);
            if(lowv > pre[u]) e.iscut = true, G[e.to][e.rev].iscut = true;
        }else if(pre[v] < pre[u] && v != fa) lowu = min(lowu, pre[v]);
    }
    return lowu;    
}

void dfs1(int u) {
    bccno[u] = bcc_cnt;
    for(int i = 0; i < G[u].size(); ++i) {
        edge &e = G[u][i]; 
        if(e.iscut || bccno[e.to]) continue;
        dfs1(e.to);
    }
}

void find_bcc() {
    memset(pre, 0, sizeof(pre));
    memset(bccno, 0, sizeof(bccno));
    memset(degree, 0, sizeof(degree));
    timestamp = bcc_cnt = block_cnt = 0;
    for(int i = 0; i < n; ++i)
        if(!pre[i]) dfs(i, -1), block_cnt++;
    for(int i = 0; i < n; ++i)
        if(!bccno[i]) bcc_cnt++, dfs1(i);
}

void Solve() {
    find_bcc();
    for(int u = 0; u < n; ++u) 
        for(int i = 0; i < G[u].size(); ++i) {
            int v = G[u][i].to;
            if(G[u][i].iscut) degree[bccno[v]]++;
        }
    int cnt = 0;
    for(int i = 1; i <= bcc_cnt; ++i)
        if(degree[i] == 1) cnt++;
        else if(degree[i] == 0) cnt += 2;
    if(bcc_cnt == 1) printf("%d\n", 0);
    else printf("%d\n", (cnt + 1) / 2);
}

inline int ReadInt() {    
    int n = 0, ch = getchar();
    while(ch < '0' || ch > '9') ch = getchar();
    do {
        n = n * 10 + ch - '0';
        ch = getchar();
    }while(ch >= '0' && ch <= '9');
    return n;
}

int main() {
    int f, t;
    while(~scanf("%d%d", &n, &m)) {
        for(int i = 0; i < n; ++i) G[i].clear();
        for(int i = 0; i < m; ++i) {
            f = ReadInt() - 1, t = ReadInt() - 1;
            G[f].push_back(edge(t, 0, G[t].size()));
            G[t].push_back(edge(f, 0, G[f].size() - 1));
        }
        Solve();
    }
}

总结

这种边－双联通的题目一般特征较明显，有直接说的，有的是无向图把边定向使得之后的图强联通的，有加边的。总之分析出“两条独立路径”这个信息，就很容易识别出来了。模版打熟，思路理解，应该就没有问题了。

Kuhn-Munkres 算法详细解析 UVa 610 - Street Directions

Sengxian's Blog