k-d树学习笔记

Published on 2016-04-27

在计算机科学里，k-d树（k-维树的缩写）是在 $k$ 维欧几里德空间组织点的数据结构。k-d树可以使用在多种应用场合，如多维键值搜索（例：范围搜寻及最邻近搜索）。k-d树是空间二分树（Binary space partitioning）的一种特殊情况。而在算法竞赛中，k-d树往往用于在二维平面内的信息检索。本文介绍算法竞赛中常用的二维 k-d树， $k$ 维可以很方便的扩展。

定义

k-d树（k-dimensional tree），是一棵二叉树，树中存储的是一些 $k$ 维数据。在一个 $k$ 维数据集合上构建一棵 k-d树代表了对该 $k$ 维数据集合构成的 $k$ 维空间的一个划分，即树中的每个结点就对应了一个 $k$ 维的超矩形区域（Hyperrectangle）。
如果觉得上面的概念难以理解，我们先从低维入手。

一维的 k-d树

对于一维的情况，所有的点都在数轴上面，此时 k-d树其实就是二叉搜索树。
二叉搜索树（Binary Search Tree，BST），是具有如下性质的二叉树：

若它的左子树不为空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不为空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉搜索树；

例如，下图是一棵二叉搜索树，其满足 BST 的性质。

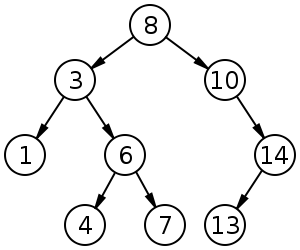
二维的 k-d树

二维的 k-d树遇到了一个问题，在一维中，坐标只有 1 维，所以我们在与根节点比较的时候，只用比较仅有的一维即可。但是二维却有 $x, y$ 坐标，如何进行比较呢？
可以这样，对于每一层，我们指定一个划分维度（轴垂直分区面 axis-aligned splitting planes），最简单就是轮流按照 $x$ 维和 y 维划分。那么假如我们这一层按照 $x$ 维划分，那么在根节点的左子树 $x$ 坐标小于根节点的 $x$ 坐标，在根节点的右子树 $x$ 坐标大于根节点的 $x$ 坐标。

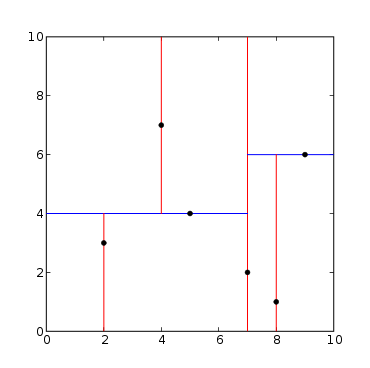
可以看到，每一次划分都用一条水平线或垂直线将平面分成了不相交的两部分。
而 k-d树的节点保存的信息我们也清楚了：

struct kdTree {
    kdTree *ch[2];
    Point p, r1, r2; //节点代表的点，子树所覆盖的矩形区域的左下角，右上角
};

k 维的 k-d树

由于三维以上我们无法想象了，但根据低维的情况不难想到， $k$ 维的 k-d树的每一层也需要确定一个维度，来对 $k$ 维空间上的点进行划分。

建树

在构造 1 维 BST 树时，一个 1 维数据根据其与树的根结点进行大小比较，来决定是划分到左子树还是右子树。
同理，我们也可以按照这样的方式，将一个 $k$ 维数据与 k-d树的根结点进行比较，只不过不是对 $k$ 维数据进行整体的比较，而是选择某一个维度 $D_i$ ，然后比较两个数据在该维度 $D_i$ 上的大小关系，即每次选择一个维度 $D_i$ 来对 $k$ 维数据进行划分，相当于用一个垂直于该维度 $D_i$ 的超平面将 $k$ 维数据空间一分为二，平面一边的所有 $k$ 维数据在 $D_i$ 维度上的值小于平面另一边的所有 $k$ 维数据对应维度上的值。
也就是说，我们每选择一个维度进行如上的划分，就会将 $k$ 维数据空间划分为两个部分，如果我们继续分别对这两个子 $k$ 维空间进行如上的划分，又会得到新的子空间，对新的子空间又继续划分，重复以上过程直到每个子空间都不能再划分为止。以上就是构造 k-d树的过程。
那么如果是二维特殊情况，就变得非常好理解了，通俗的来说就是通过过已有点的横线，竖线来划分二维平面。
上述过程中涉及到两个重要的问题：

每次对子空间的划分时，怎样确定在哪个维度上进行划分？
在某个维度上进行划分时，怎样确保在这一维度上的划分得到的两个子集合的数量尽量相等，即左子树和右子树中的结点个数尽量相等？

对于第一个问题，有很多种方法可以选择划分维度（axis-aligned splitting planes），所以有很多种创建 k-d树的方法。最典型的方法如下：
随着树的深度轮流选择维度来划分。例如，在二维空间中根节点以 x 轴划分，其子节点皆以 y 轴划分，其孙节点又以 x 轴划分，其曾孙节点则皆为 y 轴划分，依此类推。
另外的划分方法还有最大方差法（max invarince），在这里不做介绍。

而对于第二个问题，也是在 BST 中会遇到的一个问题。在 BST 中，我们是将数据的中位数作为根节点，然后再左右递归下去建树，这样可以得到一棵平衡的二叉搜索树。
同样，在 k-d树中，若在维度 $D_i$ 上进行划分时，根节点就应该选择该维度 $D_i$ 上所有数据的中位数，这样递归子树的大小就基本相同了。

bool dimension;
inline bool cmp(const Point &p1, const Point &p2) {
    if (dimension == 0) return (p1.x < p2.x) || (p1.x == p2.x && p1.y < p2.y);
    return (p1.y < p2.y) || (p1.y == p2.y && p1.x < p2.x);
}
kdTree* build(int l, int r, bool d) {
    if (l >= r) return null;
    dimension = d;
    int mid = (l + r) / 2;
    nth_element(ps + l, ps + mid, ps + r, cmp);
    kdTree *o = new kdTree(ps[mid]);
    o->ls = build(l, mid, d ^ 1), o->rs = build(mid + 1, r, d ^ 1);
    o->maintain();
    return o;
}

注意 nth_element 函数的使用

template<class _RanIt, class _Pr> inline  
    void nth_element(_RanIt _First, _RanIt _Nth, _RanIt _Last, _Pr _Pred)
template<class _RanIt> inline  
    void nth_element(_RanIt _First, _RanIt _Nth, _RanIt _Last)

对给定范围内的元素进行重新布置。使得位置的值就是所有元素第 k 小的值。并把所有不大于的值放到的前面。把所有不小于的值放到nth后面（不一定有序）。复杂度是 $O(n)$ 的。
所以建树的总复杂度为： $O(n\log n)$ 。

插入

与二叉搜索树的插入很像，二叉搜索树是单纯比较值，而 k-d树是与当前结点比较在 $D_i$ 维度上的值，来决定到底要在左子树还是在右子树插入。比较简单，复杂度： $O(\log n)$ 。

void modify(kdTree* &o, const Point &p) {
    if (o == null) {o = new kdTree(p); return;}
    int d = cmp(p, o->p) ^ 1; dimension ^= 1;
    modify(o->ch[d], p);
    o->maintain();
}

要注意的是插入以后要记得维护走过的节点子树覆盖的矩形区域。

查找

k 远点

最近点很好查询， $k$ 远点也是不难的，我们维护一个小根堆，初始向堆里面放入 $k$ 个 $-\infty$ ，然后之前的与比较就变成了与堆顶比较。

typedef long long type;
priority_queue<type, vector<type>, greater<type> > pq; //小根堆

void query(const kdTree *o, const Point &p) {
    if (o == null) return;
    type st = dis(o->p, p);
    if (st >= pq.top()) pq.pop(), pq.push(st); //大于堆顶，则弹出堆顶并更新
    type dis[2] = {o->ls->dis(p), o->rs->dis(p)};
    int d = dis[0] < dis[1];
    query(o->ch[d], p);
    if (dis[d ^ 1] >= pq.top()) query(o->ch[d ^ 1], p);  //最远都比堆顶大，才有可能更优
}

习题

光说不练假把式。细节还是得看代码的。
BZOJ 2648 & 2716：这里是曼哈顿距离最近点

//  Created by Sengxian on 4/26/16.
//  Copyright (c) 2016年 Sengxian. All rights reserved.
//  BZOJ 2648 k-d 树
#include <algorithm>
#include <iostream>
#include <cassert>
#include <cctype>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <set>
#define ls ch[0]
#define rs ch[1]
using namespace std;

inline int ReadInt() {
    static int n, ch;
    n = 0, ch = getchar();
    while (!isdigit(ch)) ch = getchar();
    while (isdigit(ch)) n = (n << 3) + (n << 1) + ch - '0', ch = getchar();
    return n;
}
const int maxn = 500000 + 3, maxm = 500000 + 3, INF = 0x3f3f3f3f;

struct Point {
    int x, y;
    Point(int x = 0, int y = 0): x(x), y(y) {}
}ps[maxn];

bool dimension;

//比较当前维度下大小关系
bool cmp(const Point &p1, const Point &p2) {
    if (dimension == 0) return p1.x < p2.x || (p1.x == p2.x && p1.y < p2.y);
    return p1.y < p2.y || (p1.y == p2.y && p1.x < p2.x);
}

//计算距离
int dis(const Point &p1, const Point &p2) {
    return abs(p1.x - p2.x) + abs(p1.y - p2.y);
}

struct kdTree *null, *pit;
struct kdTree {
    kdTree *ch[2];
    Point p, r1, r2;
    kdTree(Point p): p(p), r1(p), r2(p) {ch[0] = ch[1] = null;}
    kdTree() {}
    void* operator new(size_t) {return pit++;}
    void maintain() { //维护当前点覆盖的矩形
        r1.x = min(min(ls->r1.x, rs->r1.x), r1.x);
        r1.y = min(min(ls->r1.y, rs->r1.y), r1.y);
        r2.x = max(max(ls->r2.x, rs->r2.x), r2.x);
        r2.y = max(max(ls->r2.y, rs->r2.y), r2.y);
    }
    int dis(const Point &p) { //计算点到矩形边界的最近距离
        if (this == null) return INF;
        int res = 0;
        if (p.x < r1.x || p.x > r2.x) res += p.x < r1.x ? r1.x - p.x : p.x - r2.x;
        if (p.y < r1.y || p.y > r2.y) res += p.y < r1.y ? r1.y - p.y : p.y - r2.y;
         return res;
    }
}pool[maxn + maxm], *root;

int n, m;

void init() {
    pit = pool;
    null = new kdTree();
    null->r1 = Point(INF, INF), null->r2 = Point(-INF, -INF);
}

kdTree* build(int l, int r, bool d) {
    if (l >= r) return null;
    int mid = (l + r) / 2;
    dimension = d;
    nth_element(ps + l, ps + mid, ps + r, cmp); //使用中位数来使树尽量平衡
    kdTree *o = new kdTree(ps[mid]);
    o->ls = build(l, mid, d ^ 1), o->rs = build(mid + 1, r, d ^ 1);
    o->maintain();
    return o;
}

int ans;
void query(const kdTree* o, const Point &p) {
    if (o == null) return;
    ans = min(ans, dis(p, o->p));
    int d = o->ls->dis(p) > o->rs->dis(p); //优先递归查询点到左右儿子矩形距离小的那个
    query(o->ch[d], p);
    if (o->ch[d ^ 1]->dis(p) < ans) query(o->ch[d ^ 1], p); //如果另一个儿子有可能比当前结果小，就递归下去
}

void modify(kdTree* &o, const Point &p) {
    if (o == null) {o = new kdTree(p); return;}
    int d = cmp(p, o->p) ^ 1; dimension ^= 1;
    modify(o->ch[d], p);
    o->maintain();
}

int main() {
    init();
    n = ReadInt(), m = ReadInt();
    for (int i = 0; i < n; ++i)
        ps[i].x = ReadInt(), ps[i].y = ReadInt();
    root = build(0, n, 0);
    while (m--) {
        int type = ReadInt(), x = ReadInt(), y = ReadInt();
        if (type == 1) {
            dimension = 0;
            modify(root, Point(x, y));
        } else if (type == 2) {
            ans = INF;
            query(root, Point(x, y));
            printf("%d\n", ans);
        }
    }
    return 0;
}

BZOJ 2626：欧几里得距离 $k$ 远点

//  Created by Sengxian on 4/27/16.
//  Copyright (c) 2016年 Sengxian. All rights reserved.
//  BZOJ 2648 k-d 树
#include <algorithm>
#include <iostream>
#include <cassert>
#include <cctype>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#define ls ch[0]
#define rs ch[1]
using namespace std;

inline int ReadInt() {
    static int n, ch;
    static bool flag;
    n = 0, ch = getchar(), flag = false;
    while (!isdigit(ch)) flag |= ch == '-', ch = getchar();
    while (isdigit(ch)) n = (n << 3) + (n << 1) + ch - '0', ch = getchar();
    return flag ? -n : n;
}

typedef double type;
const int maxn = 100000 + 3;
const type INF = 1e300;
struct Point {
    int x, y, id;
    Point(int x = 0, int y = 0, int id = 0): x(x), y(y), id(id) {}
}ps[maxn];

bool dimension;

inline bool cmp(const Point &p1, const Point &p2) {
    if (dimension == 0) return (p1.x < p2.x) || (p1.x == p2.x && p1.y < p2.y);
    return (p1.y < p2.y) || (p1.y == p2.y && p1.x < p2.x);
}

inline type dis(const Point &p1, const Point &p2) {
    return (type)(p1.x - p2.x) * (p1.x - p2.x) + (type)(p1.y - p2.y) * (p1.y - p2.y);
}

struct kdTree *null, *pit;
struct kdTree {
    kdTree *ch[2];
    Point p, r1, r2;
    kdTree(const Point &p): p(p), r1(p), r2(p) {ch[0] = ch[1] = null;}
    kdTree() {}
    void* operator new(size_t) {return pit++;}
    inline void maintain() {
        r1.x = min(min(ls->r1.x, rs->r1.x), r1.x);
        r1.y = min(min(ls->r1.y, rs->r1.y), r1.y);
        r2.x = max(max(ls->r2.x, rs->r2.x), r2.x);
        r2.y = max(max(ls->r2.y, rs->r2.y), r2.y);
    }
    inline type dis(const Point &p) {
        if (this == null) return -INF;
        return max(max(::dis(p, r1), ::dis(p, r2)), max(::dis(p, Point(r1.x, r2.y)), ::dis(p, Point(r2.x, r1.y))));
    }
}pool[maxn], *root;

void init() {
    pit = pool;
    null = new kdTree();
    null->r1 = Point(0x3f3f3f3f, 0x3f3f3f3f), null->r2 = Point(-0x3f3f3f3f, -0x3f3f3f3f);
}

kdTree* build(int l, int r, bool d) {
    if (l >= r) return null;
    dimension = d;
    int mid = (l + r) / 2;
    nth_element(ps + l, ps + mid, ps + r, cmp);
    kdTree *o = new kdTree(ps[mid]);
    o->ls = build(l, mid, d ^ 1), o->rs = build(mid + 1, r, d ^ 1);
    o->maintain();
    return o;
}

struct state {
    type dis;
    int id;
    state(type dis = 0, int id = 0): dis(dis), id(id) {}
    bool operator < (const state &s) const {
        return dis > s.dis || (dis == s.dis && id < s.id);
    }
};
priority_queue<state> pq; //小根堆

void query(const kdTree *o, const Point &p) {
    if (o == null) return;
    state st = state(dis(o->p, p), o->p.id);
    if (st < pq.top()) {pq.pop(); pq.push(st);} //如果距离比堆顶大，立即更新
    type dis[2] = {o->ls->dis(p), o->rs->dis(p)};
    int d = dis[0] < dis[1]; //选距离较大的那个！
    query(o->ch[d], p);
    if (state(dis[d ^ 1], o->ch[d ^ 1]->p.id) < pq.top()) query(o->ch[d ^ 1], p); //如果距离比可能堆顶大，那么就可以递归下去
}

int n, m;

int main() {
    #ifndef ONLINE_JUDGE
        freopen("test.in", "r", stdin);
    #endif
    init();
    n = ReadInt();
    for (int i = 0; i < n; ++i) ps[i].x = ReadInt(), ps[i].y = ReadInt(), ps[i].id = i;
    root = build(0, n, 0);
    m = ReadInt();
    while (m--) {
        int x = ReadInt(), y = ReadInt(), k = ReadInt();
        while (!pq.empty()) pq.pop();
        for (int i = 0; i < k; ++i) pq.push(state(-INF, 0));
        query(root, Point(x, y));
        printf("%d\n", pq.top().id + 1);
    }
    return 0;
}

BZOJ 4520：欧几里得距离 $k$ 远点对，注意会重复，所以变成 $2k$ 。

//  Created by Sengxian on 4/27/16.
//  Copyright (c) 2016年 Sengxian. All rights reserved.
//  BZOJ 4520 k-d 树
#include <algorithm>
#include <iostream>
#include <cassert>
#include <cctype>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#define ls ch[0]
#define rs ch[1]
using namespace std;

inline int ReadInt() {
    static int n, ch;
    n = 0, ch = getchar();
    while (!isdigit(ch)) ch = getchar();
    while (isdigit(ch)) n = (n << 3) + (n << 1) + ch - '0', ch = getchar();
    return n;
}

typedef long long type;
const int maxn = 100000 + 3;
const type INF = 0x3f3f3f3f3f3f3f3fLL;
struct Point {
    int x, y;
    Point(int x = 0, int y = 0): x(x), y(y) {}
}ps[maxn];

bool dimension;

inline bool cmp(const Point &p1, const Point &p2) {
    if (dimension == 0) return (p1.x < p2.x) || (p1.x == p2.x && p1.y < p2.y);
    return (p1.y < p2.y) || (p1.y == p2.y && p1.x < p2.x);
}

inline type dis(const Point &p1, const Point &p2) {
    return (type)(p1.x - p2.x) * (p1.x - p2.x) + (type)(p1.y - p2.y) * (p1.y - p2.y);
}

struct kdTree *null, *pit;
struct kdTree {
    kdTree *ch[2];
    Point p, r1, r2;
    kdTree(const Point &p): p(p), r1(p), r2(p) {ch[0] = ch[1] = null;}
    kdTree() {}
    void* operator new(size_t) {return pit++;}
    inline void maintain() {
        r1.x = min(min(ls->r1.x, rs->r1.x), r1.x);
        r1.y = min(min(ls->r1.y, rs->r1.y), r1.y);
        r2.x = max(max(ls->r2.x, rs->r2.x), r2.x);
        r2.y = max(max(ls->r2.y, rs->r2.y), r2.y);
    }
    inline type dis(const Point &p) {
        if (this == null) return -INF;
        return max(max(::dis(p, r1), ::dis(p, r2)), max(::dis(p, Point(r1.x, r2.y)), ::dis(p, Point(r2.x, r1.y))));
    }
}pool[maxn], *root;

void init() {
    pit = pool;
    null = new kdTree();
    null->r1 = Point(0x3f3f3f3f, 0x3f3f3f3f), null->r2 = Point(-0x3f3f3f3f, -0x3f3f3f3f);
}

kdTree* build(int l, int r, bool d) {
    if (l >= r) return null;
    dimension = d;
    int mid = (l + r) / 2;
    nth_element(ps + l, ps + mid, ps + r, cmp);
    kdTree *o = new kdTree(ps[mid]);
    o->ls = build(l, mid, d ^ 1), o->rs = build(mid + 1, r, d ^ 1);
    o->maintain();
    return o;
}

priority_queue<type, vector<type>, greater<type> > pq; //小根堆

void query(const kdTree *o, const Point &p) {
    if (o == null) return;
    type st = dis(o->p, p);
    if (st >= pq.top()) pq.pop(), pq.push(st);
    type dis[2] = {o->ls->dis(p), o->rs->dis(p)};
    int d = dis[0] < dis[1];
    query(o->ch[d], p);
    if (dis[d ^ 1] >= pq.top()) query(o->ch[d ^ 1], p);
}

int n, k;

int main() {
    #ifndef ONLINE_JUDGE
        freopen("test.in", "r", stdin);
    #endif
    init();
    n = ReadInt(), k = ReadInt();
    for (int i = 0; i < n; ++i) ps[i].x = ReadInt(), ps[i].y = ReadInt();
    root = build(0, n, 0);
    while (!pq.empty()) pq.pop();
    for (int i = 0; i < 2 * k; ++i) pq.push(-1);
    for (int i = 0; i < n; ++i) query(root, ps[i]);
    printf("%lld\n", pq.top());
    return 0;
}

BZOJ 4521 - [Cqoi2016]手机号码 BZOJ 4540 - [Hnoi2016]序列