KMP 算法详细解析
Published on 2015-11-14虽然说网上 KMP 算法的解析实在是太多太多,可我还是忍不住要写一篇,因为我不想用那些看似逼格满满,却将简单事情搞得超级复杂的式子来说明。
下面,请带着轻松的心情来看这篇文章。
字符串匹配算法
字符串匹配是计算机的进行的非常频繁的算法。简单的说,有一个字符串 I have a dream. 。我想知道的事情是,里面是否包含另一个字符串 dream ?
因为执行的非常频繁,所以算法的效率也就十分重要。而本文所说的KMP算法,无疑是速度上面的佼佼者,它可以在 的时间完成匹配。
KMP算法由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称KMP算法)
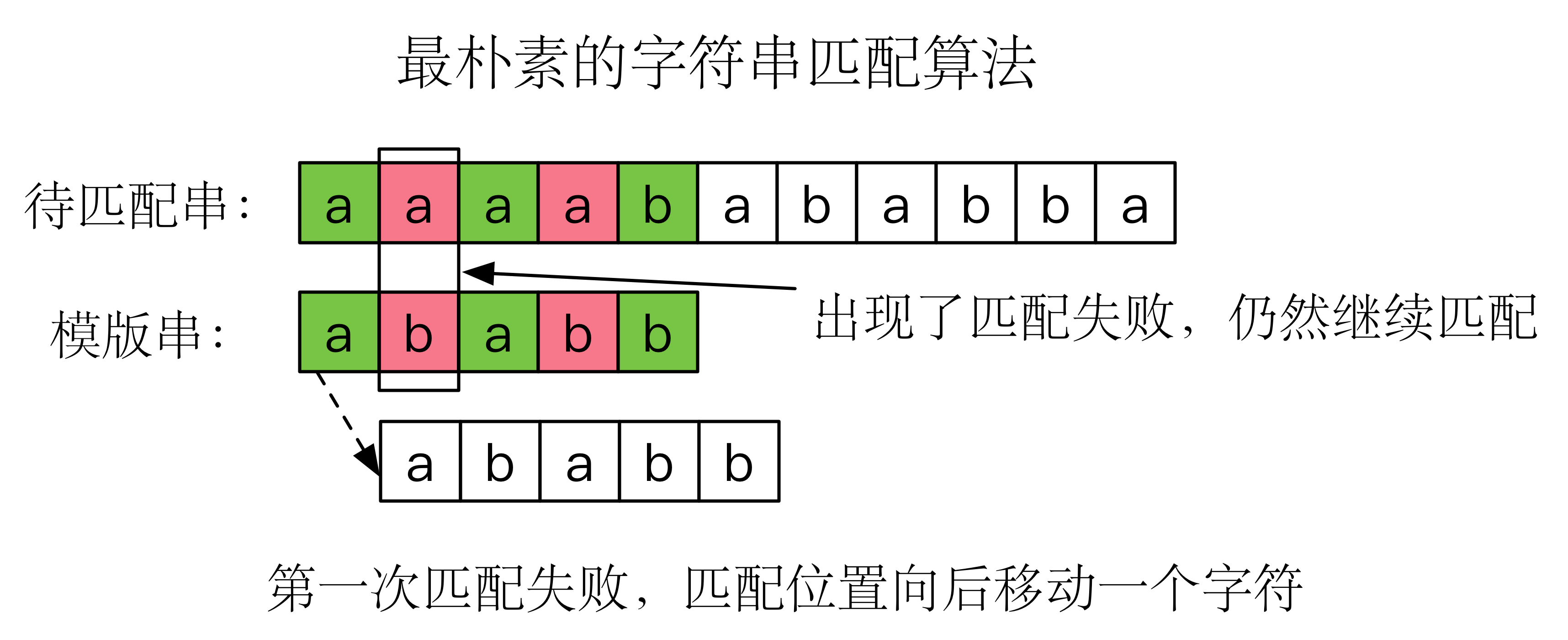
朴素的匹配方法
谈到KMP算法,就理所应当先说一说朴素的匹配方法。设待匹配串长度为 ,模版串长度为 。
最朴素的方法就是依次从待匹配串的每一个位置开始,逐一与模版串匹配,因为最多检查 个位置,所以方法的复杂度为 。
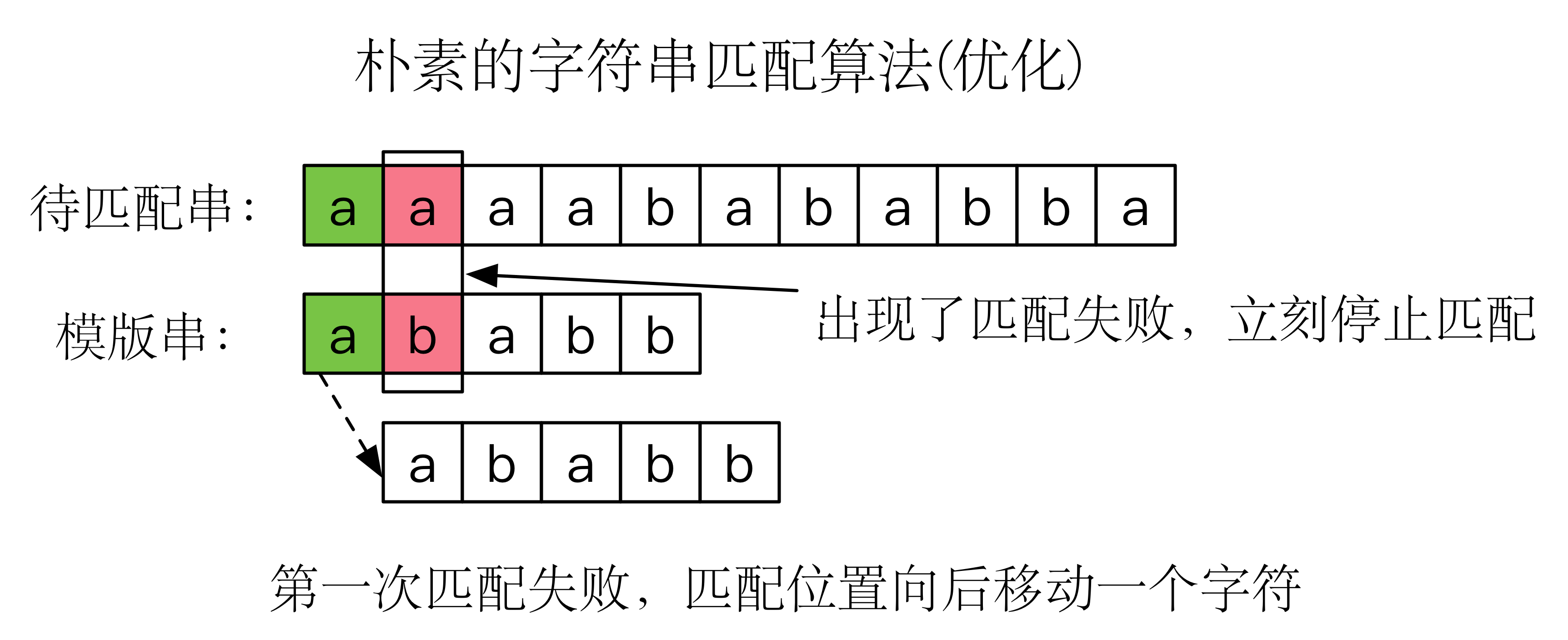
不难想到一个简单的优化,就是在比对的过程中,只要遇到有一个字符不一样,就立即停止匹配。即使这样,最坏的时间复杂度仍然是 ,然而,这种方法对于随机数据的表现相当出色,因为会频繁的停止比较。
KMP算法
假如在匹配的过程中发现正在比较的两个字符不同(称之为失配),那么朴素的算法会将模版串右移一位,重新比较。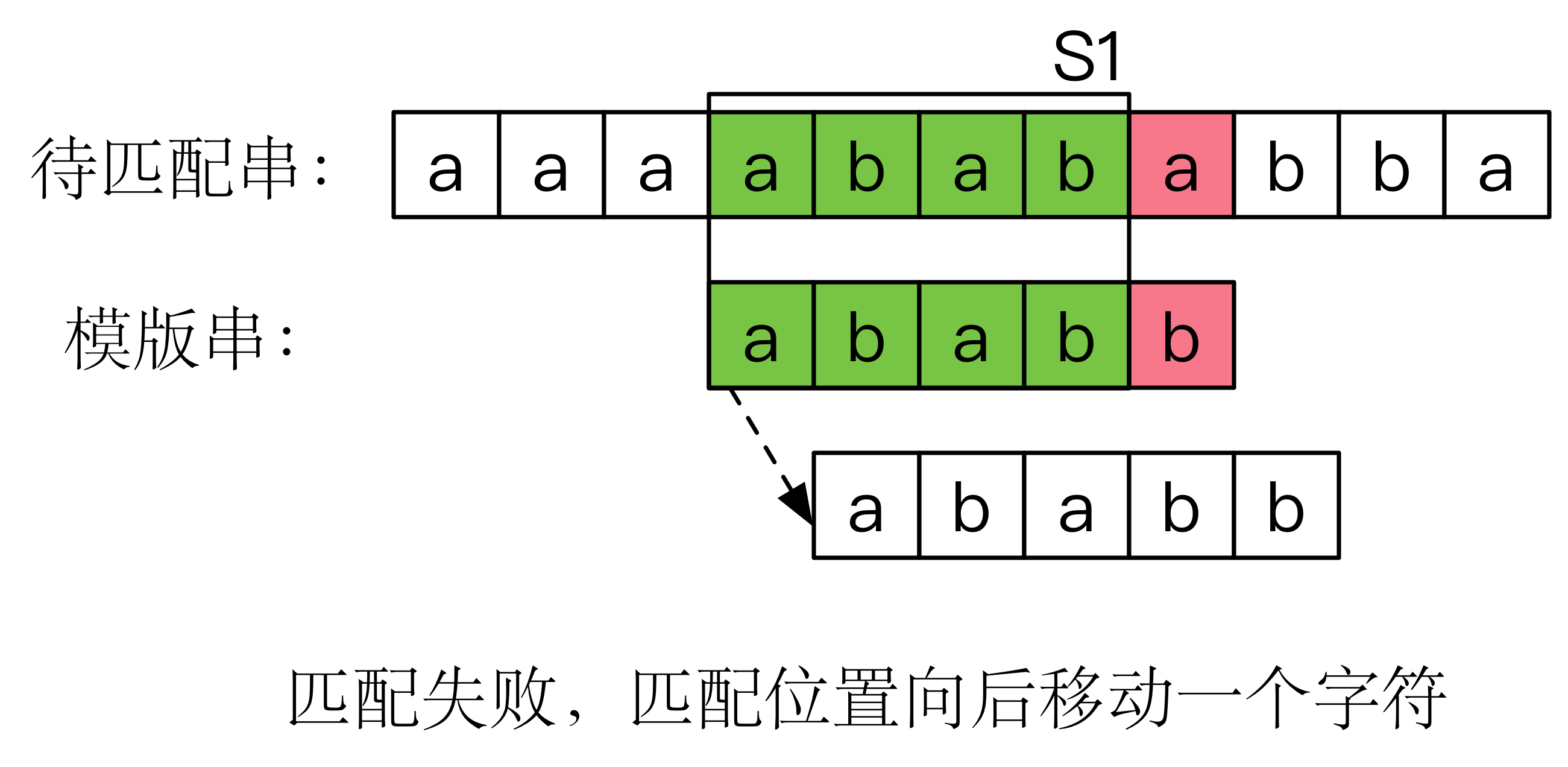
而KMP算法认为,既然失配部分前面的字符(区域S1)已经比较过了,那么就不应该再比较一次。我们已经知道S1部分就是 abab,如果后移动一个字符,a与b肯定不能匹配。
后移2位是可以的,因为模版串的前两个字符 ab 正好对齐S1的后两个字符 ab ,我们可以发现,这样的移动跟待匹配串是没有任何关系的,只要模版串中的失配点确定,那么对应后移的位数也随之确定。
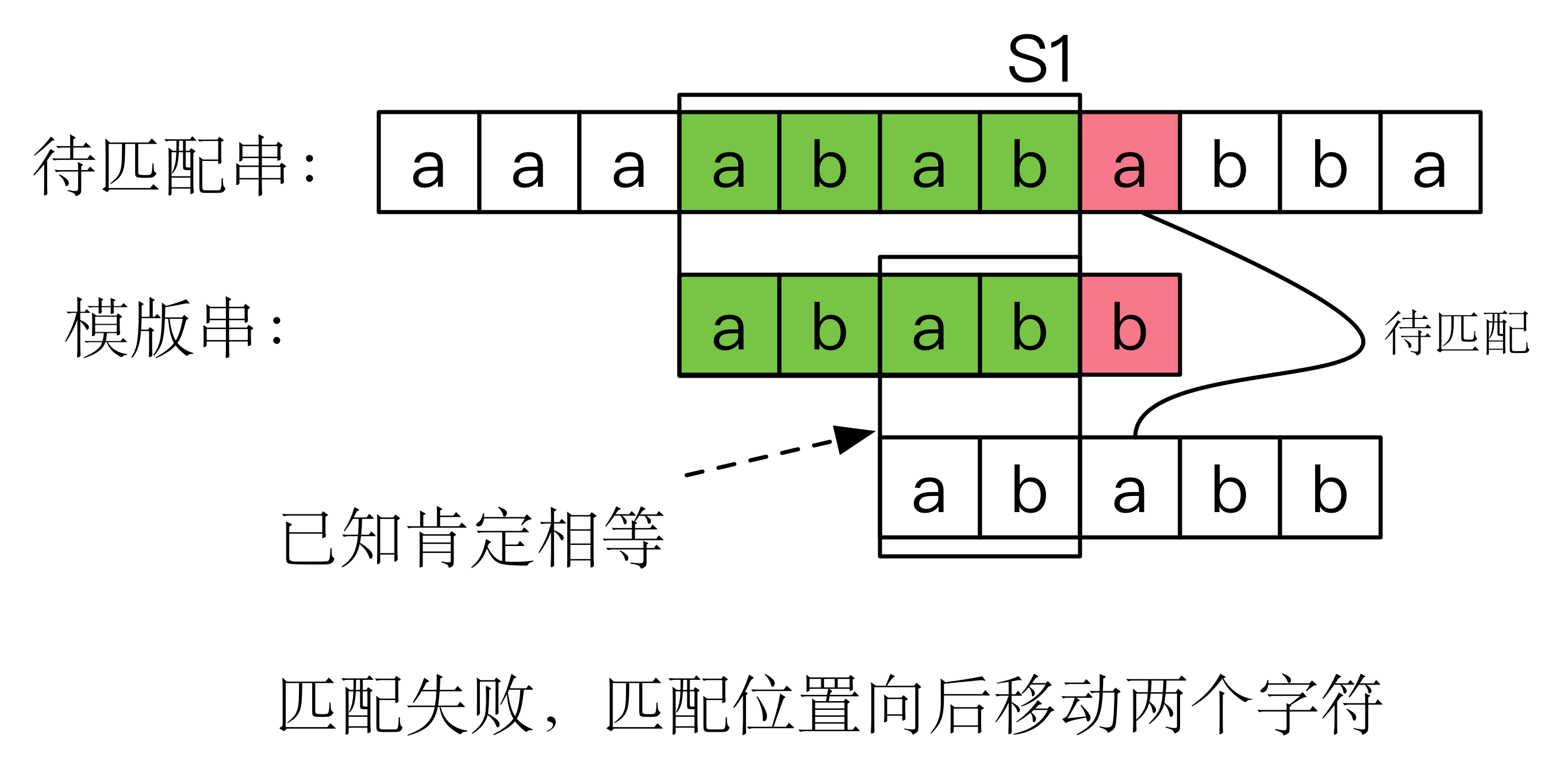
所以我们可以知道,当模版串的第5个位置发生失配时,待匹配串的失配点之前的4个字符一定是 abab,可以把待匹配串中的失配点改为与模版串的第3个位置进行匹配(相当于模版串后移2个字符)。而不管待匹配串是怎么样的,只要是在模版串的第5个位置发生失配,我们都可以把待匹配串的失配点与模版串的第三个位置匹配。
我们可以制作一张表,表示已知模版串中的失配点,待匹配串中的失配字符应该再与模版串的第几个字符再来匹配。
| 对应字符 | a | b | a | b | b | 无 |
|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
| 转移值 | 0 | 0 | 0 | 1 | 2 | 0 |
事实上,用 表示模版串中的失配点 所对应的转移值,那么模版串右移的位数就是
算法实现
假设我们通过某些手段(process 函数),拥有了这样一张失配表,那么我们就可以写出 KMP 算法的程序来。
void findstr(const char *str, const char *temp, int *f) { int n = strlen(str), m = strlen(temp); process(temp, f); //预处理得到失配表 int j = 0; //j表示当前模版串的待匹配位置 for(int i = 0; i < n; ++i) { while(j && str[i] != temp[j]) j = f[j]; //不停的转移,直到可以匹配或者走到0 if(str[i] == temp[j]) j++; //如果相等,模版串中待匹配位置可以移一位了。 if(j == m) printf("%d\n", i - m + 1); } }
考虑模版串 ababc。
构造失配表:
| 对应字符 | a | b | a | b | c | 无 |
|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
| 转移值 | 0 | 0 | 0 | 1 | 2 | 0 |
KMP 算法的精髓就蕴藏在下图中:
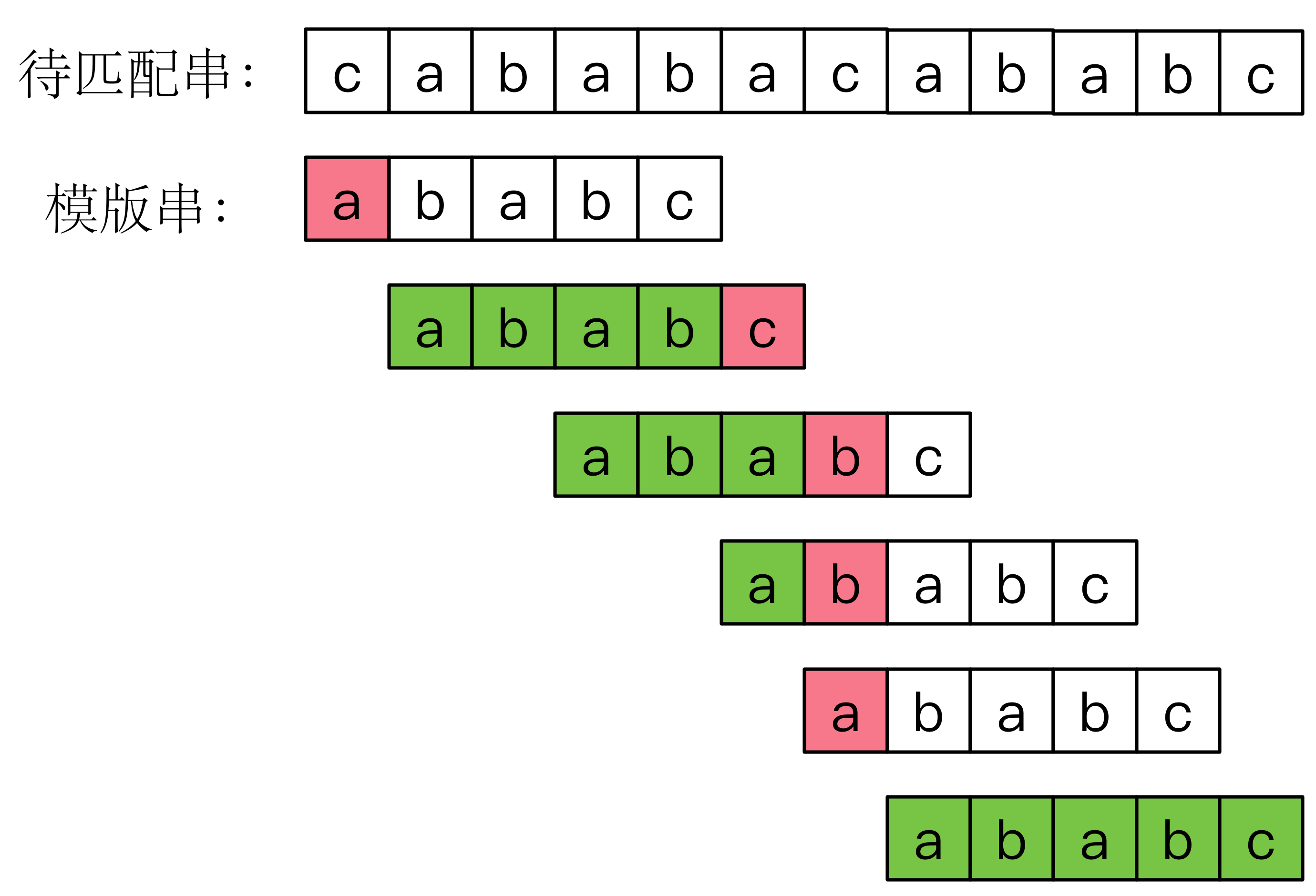
而且这个算法是可以在
ababab 中成功匹配 abab 2次的,想一想,为什么?(注意下标为4的转移值)
计算失配表
然而说了那么多,都必须有一张失配表才行,没有失配表,KMP算法是无法运行的。
在计算失配表之前,我们必须清楚一个事实。
对于失配点 来说,找到应该转移的点就像是从 向后,同时从 向前,找一段公共部分,而且这公共部分要尽可能的大,得到了这个公共部分的长度 之后,要转移到的值正好就是 。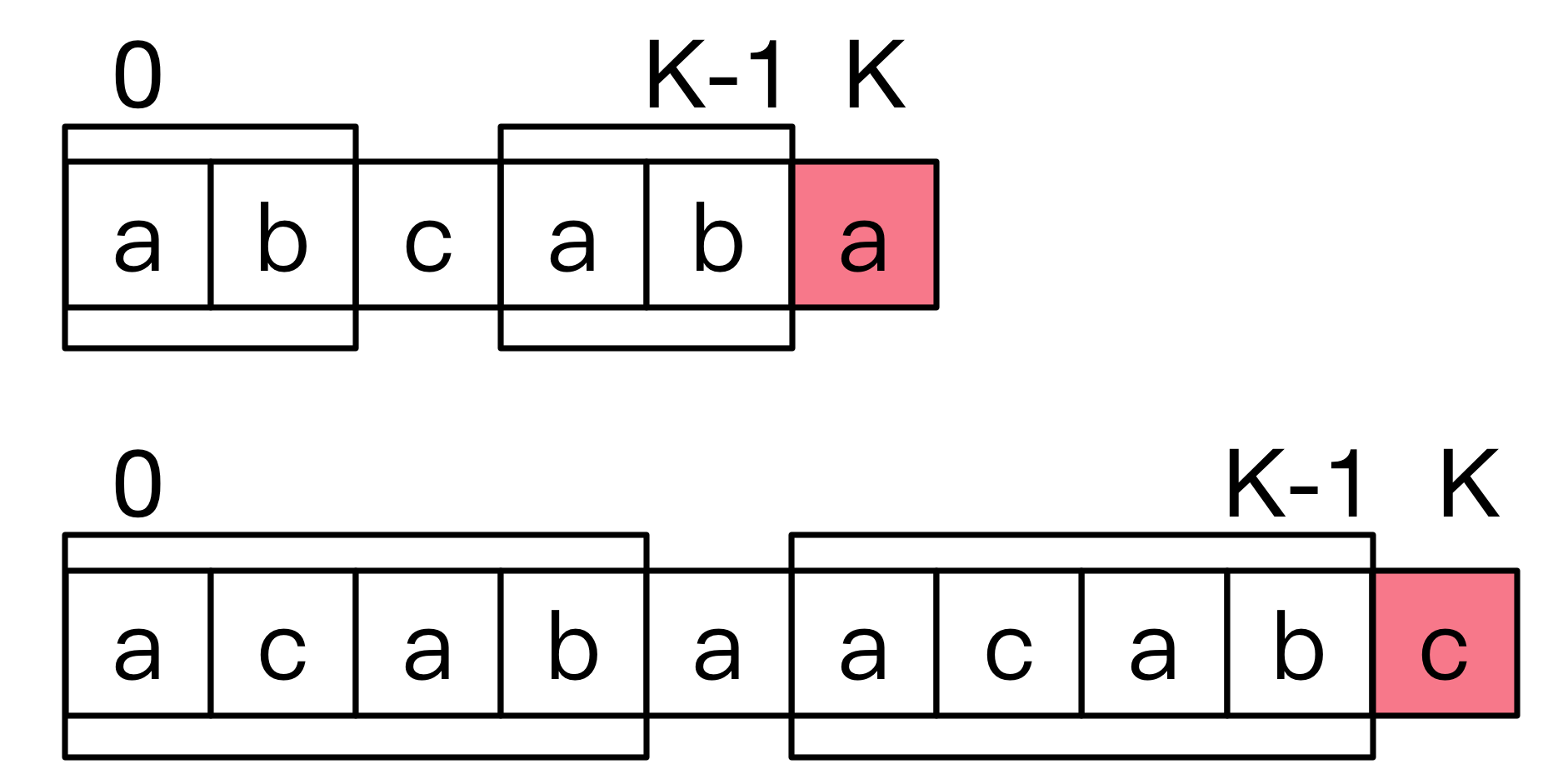
通过这个想法,我们可以在最坏 的时间内计算出失配表,而这显然是不够的。我们可以通过递推的方法算出失配表。
边界 。
如果我们已经计算出了 ,如果 ,则有 ,想象窗口(图中的矩形)同时向右扩大一格的情况。
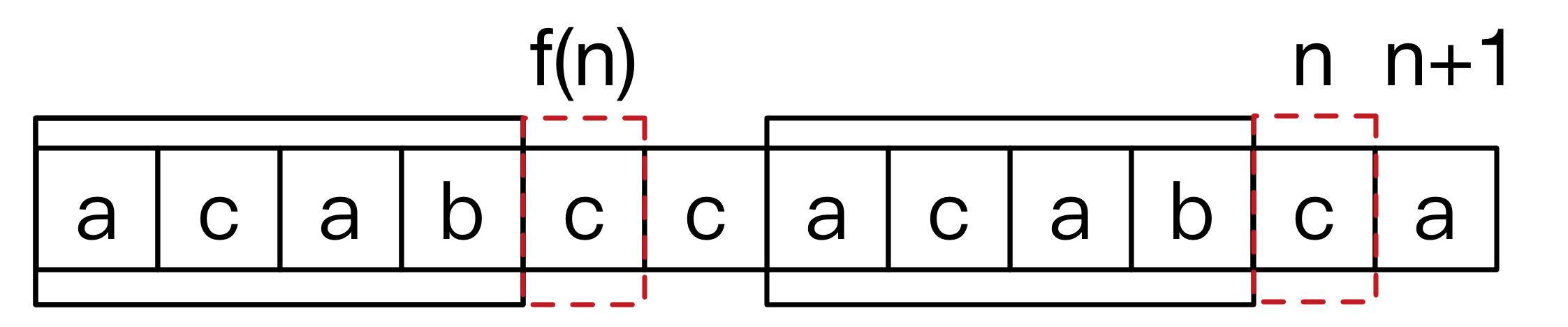
那么如果 怎么办呢?我们就要退一步考虑了,考虑是否等于 ,如果等于的话 ,不等于则再退一步,直到相等或者到0了。
为什么是正确的呢?回归本源,我们要找两个最大的窗口,而且两个窗口内的值相等,既然 ,窗口无法扩大,只好退而求其次,缩小窗口,但又要保证窗口相等,怎么办呢?当然是回溯到 ,如果 ,那么窗口就可以在 的基础上大一格啦。仔细想一想,找相等窗口的过程,像不像之前KMP的过程呢?这里是自己匹配自己。下图给出了自己匹配自己的精髓所在。
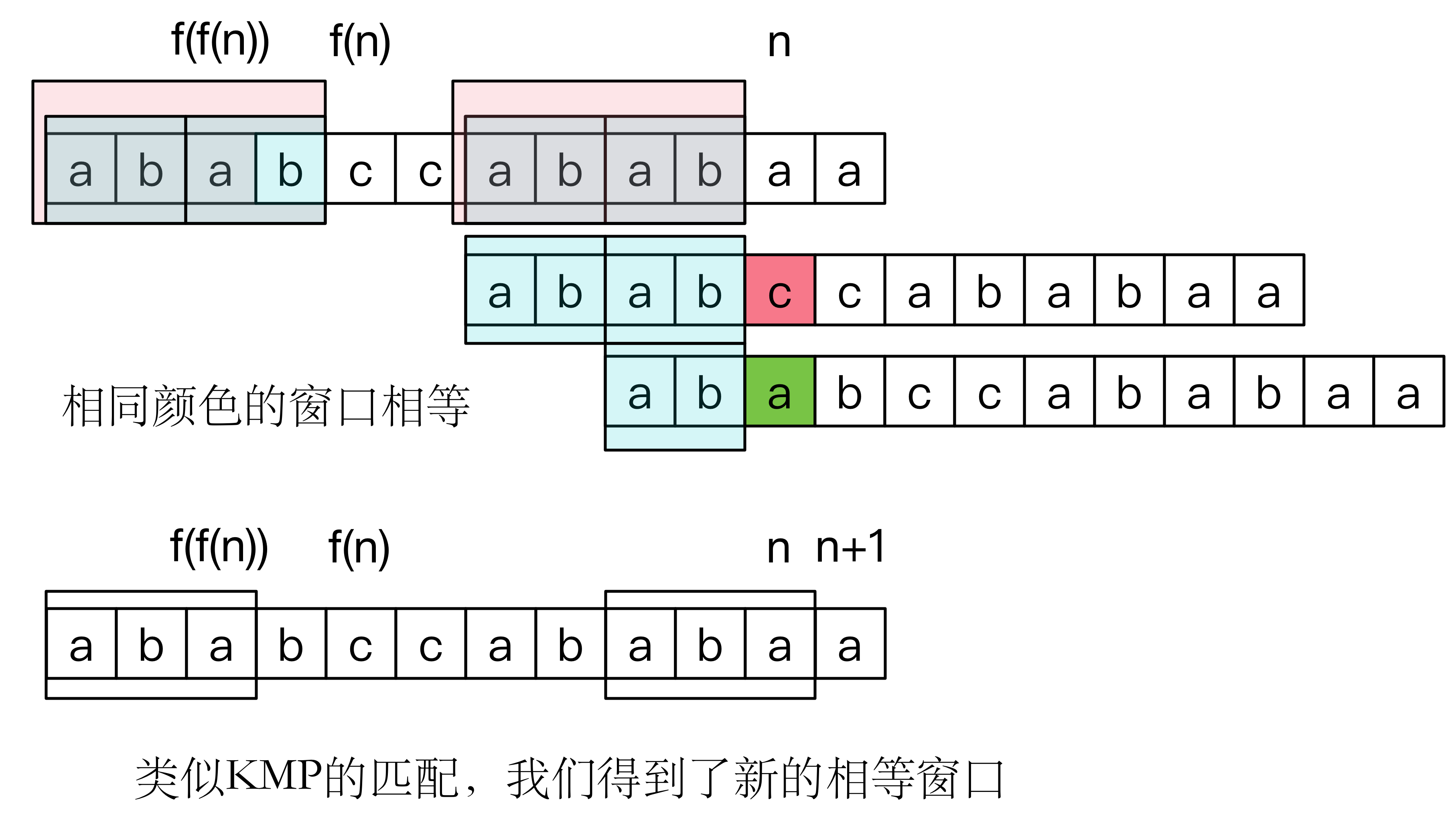
用笔推一下,试着替换某些的字符,看看为什么是这样。
算法水到渠成
void process(const char *temp, int *f) { int n = strlen(temp); f[0] = f[1] = 0; //边界 for(int i = 1; i < n; ++i) { int j = f[i]; while(j && temp[i] != temp[j]) j = f[j]; //一旦回到1,表明窗口大小为0了,只能回到最初的字符 f[i + 1] = temp[i] == temp[j] ? j + 1: 0; } }
至于复杂度的分析,比较复杂,要用到均摊分析,这里不赘述了。
总结
KMP算法的精髓在于对已知信息的充分利用,这体现在待匹配串的匹配上面,更用于预处理时自己匹配自己上面,总而言之,KMP算法是非常值得学习的。
