Sengxian's Blog

终于学了一波莫比乌斯反演，感觉一些技巧还是容易忘的，记一下方便回顾。

莫比乌斯函数

定义

莫比乌斯函数 $\mu(n)$ 的定义：
设 $n = p_1 ^ {k_1} \cdot p_2 ^ {k_2} \cdot\cdots\cdot p_m ^ {k_m}$，其中 $p$ 为素数，则定义如下：

可知有平方因子的数的莫比乌斯函数值为 $0$。

性质

性质一：莫比乌斯函数是积性函数。

应用：根据这一性质，我们可以采取线性筛法，用 $O(n)$ 的时间预处理出所有 $[1, n]$ 内的莫比乌斯函数值。
质数的值为 $-1$，如果一个数存在某个质因子的指数不为 $1$，那么它将会被筛为 $0$（值得注意的是，只有数存在最小质因子的指数大于 $1$ 时，它才会被直接筛为 $0$，其余的情况是由 $\mu(d) = -\mu(i)$ 来完成的）。
每个数仅被其最小质因子筛去，故复杂度为 $O(n)$。

void sieve() {
    fill(isPrime, isPrime + maxn, 1);
    mu[1] = 1, num = 0;
    for (int i = 2; i < maxn; ++i) {
        if (isPrime[i]) primes[num++] = i, mu[i] = -1;
        static int d;
        for (int j = 0; j < num && (d = i * primes[j]) < maxn; ++j) {
            isPrime[d] = false;
            if (i % primes[j] == 0) {
                mu[d] = 0;
                break;
            } else mu[d] = -mu[i];
        }
    }
}

性质二：

证明：当 $n = 1$ 时有 $\mu(1) = 1$，显然成立。否则设 $n = p_1 ^ {k_1} \cdot p_2 ^ {k_2} \cdot\cdots\cdot p_m ^ {k_m}$，$d = p_1 ^ {x_1} \cdot p_2 ^ {x_2} \cdot\cdots\cdot p_m ^ {x_m}$ 根据 $\mu$ 的定义，只需考虑 $x_i = 0$ 或 $x_i = 1$ 的情况。我们设 $d$ 中存在 $r$ 个 $x_i$ 为 1，那么有：

根据二项式定理：

我们令 $x = 1, y = -1$，即得证：

此公式运用的很多，在求 $\gcd = 1$ 或是用杜教筛求前缀和的时候都用的到。

莫比乌斯反演

公式

如果 $f(n), g(n)$ 是数论函数，且满足：

则有莫比乌斯反演：

证明：

根据莫比乌斯函数的性质 2，可知当且仅当 $i = n$ 时和式的值为 $g(n)$，否则为 $0$。

变形

证明就略过了，与上面的证明大同小异，可以做为练习加深理解。

应用

所有和式默认 $n\le m$，不满足则交换。

求 gcd = k 的个数

设 $f(k)$ 为 $\gcd(i, j) = k$ 的个数，$g(k)$ 为满足 $k\mid\gcd(i, j)$ 的对数，则有以下关系：

我们只需快速求出 $g(k)$，可知，如果 $i, j$ 能被 $k$ 整除，那么它们可以写成 $i = k\cdot x_1, j = k\cdot x_2$ 的形式，我们只需求有多少对 $x_1, x_2$ 即可，可得：

根据莫比乌斯反演的变形，可求得 $f(k)$：

显然 $f(k)$ 就是答案，暴力求是 $O(n)$ 的。如何快速求？这里很重要的思想就是分块，$\left\lfloor\frac n d\right\rfloor$ 有至多 $O(\sqrt n)$ 个取值。

证明：当 $1\le d< \sqrt n$ 时，由于 $d$ 只有 $\sqrt n$ 个，所以 $\left\lfloor\frac n d\right\rfloor$ 也只有至多 $\sqrt n$ 个取值。
当 $\sqrt n\le d\le n$ 时，由于 $\left\lfloor\frac n d\right\rfloor$ 小于 $\sqrt n$，所以 $\left\lfloor\frac n d\right\rfloor$ 也只有至多 $\sqrt n$ 个取值。
$\left\lfloor\frac n d\right\rfloor$ 有至多 $O(\sqrt n)$ 个取值，证明完毕。

同理 $\left\lfloor\frac m d\right\rfloor$ 也只有至多 $\sqrt m$ 个取值，又因为取值是连续的，所以 $\left\lfloor\frac n {kx}\right\rfloor$ 与 $\left\lfloor\frac m {kx}\right\rfloor$ 同时不变的段数有 $O(\sqrt n + \sqrt m)$ 个。

例：$n = 32, m = 40, k = 2$，红色为相等的段。

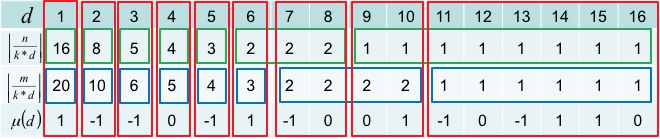
对于相等的段，我们求取 $\mu$ 的前缀和，即可批量计算这一个段的答案。

ll F(int n, int m, int d) {
    if (n > m) swap(n, m);
    ll ans = 0;
    n /= d, m /= d;
    for (int i = 1, last = 1; i <= n; i = last + 1) {
        last = min(n / (n / i), m / (m / i));
        ans += (ll)(sum[last] - sum[i - 1]) * (n / i) * (m / i);
    } 
    return ans;
}

对于位置 $i$，找到下一个相等的位置的代码为 min(n / (n / i), m / (m / i))。对于 $n$ 来说，我们要找到最大的 $j$，满足：

可以拆掉左边的底：

继续化简：

所以 $j = \left\lfloor\frac n {\lfloor\frac n i\rfloor}\right\rfloor$，对 $m$ 同理，取两个 $j$ 最小值即为都不变的段 $[i, j]$。

总之，复杂度为 $O(\sqrt n + \sqrt m)$。
这个 $f(k)$ 以及分块非常重要，几乎题题都会用到。

gcd(i, j) 的幂

按照我们刚刚的技巧，枚举最大公约数 $d$ 然后转换为可分块的形式：

到这里可以分套分块 $O((\sqrt n)^2) = O(n)$，如果多组询问怎么办呢？另一重要技巧就是枚举 $dx$，你可能会疑惑，$d, x$ 都没定呢，怎么枚举 $dx$？实际上我们枚举的是乘积，让 $dx$ 为定值，这个情况下再枚举 $d$。

原式可化为：

这样的求出答案是正确的吗？我们知道之前一步的式子是：$\sum_{d = 1}^nd^k\sum_{x=1}^{\left\lfloor\frac n d\right\rfloor}\mu(x)\left\lfloor\frac n {dx}\right\rfloor\left\lfloor\frac m {dx}\right\rfloor$。

显然只要 $d$ 以及 $x$ 定了，式子的一项也就定了，于是原式也可以写成；

只要我们能枚举出所有的二元组 $(d, x)$，并把对应项乘起来，就是正确的。

如果设 $f(n) = \sum_{d \mid n}d^k\mu(\frac T d)$，则我们只需要求 $f$ 的一个前缀和就可以 $O(\sqrt n)$ 回答询问了。
发现 $d^k$ 是积性函数，根据莫比乌斯反演的性质，$f$ 也是一个积性函数，我们可以线筛 $O(n)$ 求出答案。

怎么线筛？如果对于积性函数 $f$ 来说，$f(p^k), \textrm{p is a prime}$ 能 $O(1)$ 求出的话，那么就可以 $O(n)$ 预处理了，详见 线性筛法与积性函数。
所以我们要想办法快速处理 $f(p^k)$，通常要分解质因数来考虑。

这里化一下 $f$：

总复杂度：$O(n + T\sqrt n)$。

其他技巧

题目太多了，我懒得写了。好像不少题目都是与“求 $\gcd(i, j)$ 的幂”差不多的方法，最后都变成了线筛预处理积性函数了，那就不写了，记一下化简式子中可能用到的小技巧吧。

如果 $d(n)$ 为 $n$ 的约数个数，则：

证明：设 $nm = p_1^{x_1}\cdot p_2^{x_2}\cdot p_3^{x_3}\cdots p_k^{x_k}$，且 $n = p_1^{y_1}\cdot p_2^{y_2}\cdot p_3^{y_3}\cdots p_k^{y_k}$，则 $m = p_1^{x_1 - y_1}\cdot p_2^{x_2 - y_2}\cdot p_3^{x_3 - y_3}\cdots p_k^{x_k - y_k}$。
设 $i = p_1^{a_1}\cdot p_2^{a_2}\cdot p_3^{a_3}\cdots p_k^{a_k}$，$j = p_1^{b_1}\cdot p_2^{b_2}\cdot p_3^{b_3}\cdots p_k^{b_k}$，要使 $\gcd(i, j) = 1$，必然有 $a_1$ 或 $b_1$ 为 0，如果 $a_1$ 为 0，那么 $b_1$ 有 $x_i - y_1 + 1$ 种取值；如果 $b_1$ 为 0，那么 $a_1$ 有 $y_1 + 1$ 种取值，一共有 $x_1 + 1$ 种取值，对于 $x_i$ 也如此。
所以满足条件的 $i, j$ 对数为 $\prod(x_i + 1)$，与约数定理给出的形式一样，得证。

总结

还没写完怎么就总结了
莫比乌斯反演一般来说套路比较固定，看到两个求和符号，基本上就逃不开莫比乌斯了。
求和的东西可能不同，但是一般都与 $\gcd$ 有关，枚举 $\gcd$，再使用 $\gcd = k$ 的个数 + 分块一般能 $O(n)$，将后面的部分提前 + 积性函数预处理 + 分块一般能单组 $O(\sqrt n)$。
积性函数有时不好数学证明，那么可以打表来验证，重点关注质数，质数的幂的值。
还有如果 $n, m$ 比较大的，可能需要使用杜教筛处理一下前缀和，需要一些数学功底来推导。
杜教筛我可能会新开一个笔记（填坑）。