Sengxian's Blog

题目地址

描述

汉诺塔由三根柱子（分别用 $A$, $B$, $C$ 表示）和 $n$（本题 $n\le 30$） 个大小互不相同的空心盘子组成。一开始 $n$ 个盘子都摞在柱子 $A$ 上，大的在下面，小的在上面，形成了一个塔状的锥形体。

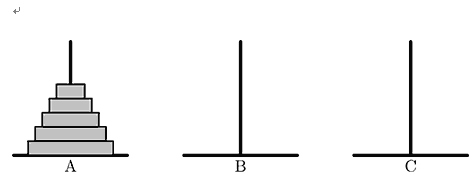
对汉诺塔的一次合法的操作是指：从一根柱子的最上层拿一个盘子放到另一根柱子的最上层，同时要保证被移动的盘子一定放在比它更大的盘子上面（如果移动到空柱子上就不需要满足这个要求）。我们可以用两个字母来描述一次操作：第一个字母代表起始柱子，第二个字母代表目标柱子。例如，AB 就是把柱子 $A$ 最上面的那个盘子移到柱子 $B$。汉诺塔的游戏目标是将所有的盘子从柱子 $A$ 移动到柱子 $B$ 或柱子 $C$ 上面。有一种非常简洁而经典的策略可以帮助我们完成这个游戏。首先，在任何操作执行之前，我们以任意的次序为六种操作（AB、AC、BA、BC、CA 和 CB）赋予不同的优先级，然后，我们总是选择符合以下两个条件的操作来移动盘子，直到所有的盘子都从柱子 $A$ 移动到另一根柱子：

1. 这种操作是所有合法操作中优先级最高的；
2. 这种操作所要移动的盘子不是上一次操作所移动的那个盘子。

可以证明，上述策略一定能完成汉诺塔游戏。现在你的任务就是假设给定了每种操作的优先级，计算按照上述策略操作汉诺塔移动所需要的步骤数。
保证答案不会超过 $10^{18}$。

分析

模拟肯定是不行的，$10^{18}$ 跑 5 个小时都跑不完。
在原版的汉诺塔问题中，步骤具有明显的递归性质，虽然本题规则有所改变，我们必须朝着递归的方向思考。
首先可以肯定的是，本题的步骤是唯一的，所以我们不需要通过动态规划来进行最优决策，任何情况下都只有一种选择。
在解题之前先提醒一下本题的一个重要信息：“这种操作所要移动的盘子不是上一次操作所移动的那个盘子”。

设 $f[j][i]$ 为 $i$ 中有 $j$ 个盘子，且除 $i$ 以外其余柱子中没有盘子，将 $i$ 中的全部盘子移到某一个盘子的最小步数，我们 $i$ 柱的盘子移到了 $g[j][i]$ 中。
显然 $f[n][0]$ 为答案（$A$ 为 0，$B$ 为 1，$C$ 为 2）。考虑边界 $f[1][i] = 1$，根据优先级，我们可以算出 $g[1][i]$，优先级仅在这一步有用。

考虑如何计算 $f[j][i]$，注意，只有 $i$ 柱有 $j$ 个盘子！为了转移 $i$ 上的 $j$ 个盘子，我们必须将 $j - 1$ 个盘子先全部移动到某个柱子上（也必定有一个时刻是这样的，否则不可能结束游戏），设移动到的柱子为 $a = g[j - 1][i]$，则另外一个柱子为 $b = 3 - i - a$。为什么可以使用 $g[j - 1][i]$ 呢？因为 $i$ 最底下最大的盘子是无用的，如果要移动它，说明有一个柱子是空的，说明已经有一个柱子上有 $j - 1$ 个盘子了，与最小步数违背！所以可以直接忽略最大的盘子。

我们知道，现在 $i$ 上有一个盘子，$a$ 上有 $j - 1$ 个盘子，而且之前一步进行的操作一定是把某个盘子移到 $a$ 上。现在只能动 $i$ 上面最大的盘子了，我们把它移到 $b$，现在又只能动 $a$ 了。
考虑 $g[j - 1][a]$ 的取值：

1. 如果 $g[j - 1][a] = b$，那么直接将 $a$ 上的 $j - 1$ 个移动到 $b$，任务完成，$g[j][i] = b$，总共的花费为 $f[j][i] + 1 + f[j - 1][a]$。
2. 如果 $g[j - 1][a] = i$，那么先将 $a$ 上的 $j - 1$ 个移动到 $i$，再将 $b$ 上最大的盘子移动到 $a$，再将 $i$ 上的 $i - 1$ 个盘子移动到 $a$，任务完成，$g[j][i] = a$，总共的花费为 $f[j - 1][i] + 1 + f[j - 1][a] + 1 + f[j - 1][i]$。

实现起来非常简单，复杂度： $O(n)$。

代码

//  Created by Sengxian on 08/23/16.
//  Copyright (c) 2016年 Sengxian. All rights reserved.
//  BZOJ 1019 递推
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int maxn = 30 + 3;
int n, g[maxn][3];
ll f[maxn][3];
bool vis[3];

int main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
#endif
    scanf("%d", &n);
    for (int i = 0; i < 6; ++i) {
        static char str[10];
        scanf("%s", str);
        int a = str[0] - 'A', b = str[1] - 'A';
        if (vis[a]) continue;
        vis[a] = true, f[1][a] = 1, g[1][a] = b;
    }
    for (int j = 2; j <= n; ++j)
        for (int i = 0, a, b; i < 3; ++i) {
            a = g[j - 1][i], b = 3 - i - a;
            if (g[j - 1][a] == b) f[j][i] = f[j - 1][i] + 1 + f[j - 1][a], g[j][i] = b;
            else f[j][i] = f[j - 1][i] + 1 + f[j - 1][a] + 1 + f[j - 1][i], g[j][i] = a;
        }
    printf("%lld\n", f[n][0]);
    return 0;
}