BZOJ 1068 - [SCOI2007]压缩

#DP
Published on 2016-06-10

题目地址

描述

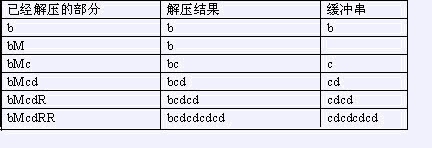
给一个由小写字母组成的字符串，我们可以用一种简单的方法来压缩其中的重复信息。压缩后的字符串除了小写字母外还可以（但不必）包含大写字母 RR 与 MM，其中 MM 标记重复串的开始，RR 重复从上一个 MM（如果当前位置左边没有 MM，则从串的开始算起）开始的解压结果（称为缓冲串）。 bcdcdcdcd 可以压缩为 bMcdRR，下面是解压缩的过程：

分析

首先明确这个题的压缩方式，类似将串不停的翻倍，比如 MaRRR 得到 aaaaaaaa，这跟循环节压缩有很大区别，所以不顾题目特性往循环节上面去想是不合理的。
这个题目的压缩方法是翻倍，意味着如果有一个子串左右两半相同，那么我们就可以压缩，但如果要利用“前一半的压缩结果”的前提是除了串的开头有 MM，其余位置是不能有 MM 的。这启发我们定三维状态。

dp[i][j][k]dp[i][j][k] 表示将 [i,j][i, j] 压缩能得到的最短长度，其中 k=0k = 0 表示没有 MM，k=1k = 1 表示无限制，则 dp[i][i][k]=1dp[i][i][k] = 1。
答案是 dp[0][n−1][1]dp[0][n - 1][1]，注意串 [0,n−1][0, n - 1] 的开头是有一个 MM 的，为了保证 dp[i][j][1]dp[i][j][1] 就是子串压缩的最优答案，我们假定所有子串前面有一个 MM（不计入答案，在转移的时候计入）。
方程为：

dp[i][j][0]=min{dp[i][k][0]+j−k,k∈[i,j)dp[i][i+j2][0]+1s[i,i+j2]=s[i+j2+1,j]dp[i][j][0] = \min\begin{cases}dp[i][k][0] + j - k, k\in [i, j)\\dp[i][\frac{i + j} 2][0] + 1 & & s_{[i, \frac{i + j} 2]} = s_{[\frac {i + j} 2 + 1, j]}\end{cases}

而 k=1k = 1 的时候要注意，枚举分割的位置，分割的位置需要放一个 MM 来保证后面的串前面有一个 MM。

dp[i][j][1]=min{dp[i][j][0]dp[i][k][1]+1+dp[k+1][j][1],k∈[i,j)dp[i][j][1] = \min\begin{cases}dp[i][j][0]\\dp[i][k][1] + 1 + dp[k + 1][j][1], k\in [i, j)\end{cases}

总结：

  1. 做题时要根据题目特性入手，而不是根据以往的经验。
  2. 有时候让 DP 的每个子状态都能独立正确，会更方便。

代码

//  Created by Sengxian on 6/10/16.
//  Copyright (c) 2016年 Sengxian. All rights reserved.
//  BZOJ 1068 区间DP 字符串压缩
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
inline int ReadInt() {
    static int n, ch;
    n = 0, ch = getchar();
    while (!isdigit(ch)) ch = getchar();
    while (isdigit(ch)) n = (n << 3) + (n << 1) + ch - '0', ch = getchar();
    return n;
}

const int maxn = 50 + 3;
int n, dp[maxn][maxn][2];
char str[maxn];

inline bool judge(char *str, int n) {
    if (n & 1) return false;
    int ha = n >> 1;
    for (int i = 0; i < ha; ++i)
        if (str[i] != str[i + ha]) return false;
    return true;
}

int main() {
    scanf("%s", str);
    n = strlen(str);
    memset(dp, 0x3f, sizeof dp);
    for (int i = 0; i < n; ++i) dp[i][i][0] = 1, dp[i][i][1] = 1;
    for (int w = 2; w <= n; ++w)
        for (int i = 0; i + w <= n; ++i) {
            int j = i + w - 1;
            for (int k = i; k < j; ++k) {
                dp[i][j][0] = min(dp[i][j][0], dp[i][k][0] + j - k);
                dp[i][j][1] = min(dp[i][j][1], dp[i][k][1] + 1 + dp[k + 1][j][1]);
//                dp[i][j][1] = min(dp[i][j][1], dp[i][k][1] + min(j - k, 1 + dp[k + 1][j][1])); //不需要这样，因为如果前面没有 M，意味着 dp[i][j][0] 可以更新到最优答案，否则有 M，那么一定会枚举放 M 的正确位置
            }
            if (judge(str + i, w)) dp[i][j][0] = min(dp[i][j][0], dp[i][i + (w >> 1) - 1][0] + 1); 
            dp[i][j][1] = min(dp[i][j][0], dp[i][j][1]);
        }
    printf("%d\n", dp[0][n - 1][1]);
    return 0;
}
BZOJ 3928 - [Cerc2014] Outer space invaders