BZOJ 4105 - [Thu Summer Camp 2015]平方运算

#数论 #线段树
Published on 2016-06-01

题目地址

描述

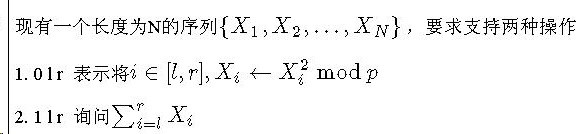
分析

既然每次 XiX_i 都要模 pp，那么我们可以想到，是否对于任意 Xi→Xi2modPX_i \rightarrow X_i^2 \bmod P，都可以很快的发生循环呢？

事实上，经过打表，根据题目所给的模数，任意数经过至多 11 步就可以进入环！同时打表发现每个环的长度小于 60！这启发我们用类似 BZOJ 3038 的方式思考。
在 BZOJ 3038 中，要求给 [l,r][l, r] 中的每个数 xx 变为 x\sqrt x，并支持区间求和操作。发现显然 0,10, 1 怎么开根号都不变，而 xx 至多需要 log2lgx\log_2\lg x 次就可以变为 1。所以用线段树维护，遇到修改，如果区间全为 0,10, 1，就不管，否则暴力开根，可以发现均摊复杂度是很低的。

在本题中，我们仍然可以用线段树维护，在线段树上分解区间，如果区间里面的所有数都在环中，那么这个区间节点维护所有数的环的 ，环上的第 ii 个节点维护若这个区间进行 ii 次平方操作，和是多少。
遇到一个修改，如果区间所有数在环中，那么在环上走一位即可，否则暴力平方，因为至多 11 步就可进入环，那么均摊下来复杂度是很低的。

实现方面，线段树的各种标记处理应该是基本功了，如果不太熟练的话可以看看我的代码。

代码

//  Created by Sengxian on 6/1/16.
//  Copyright (c) 2016年 Sengxian. All rights reserved.
//  BZOJ 4105 线段树 + 数论
#include <bits/stdc++.h>
using namespace std;

inline int ReadInt() {
    static int n, ch;
    n = 0, ch = getchar();
    while (!isdigit(ch)) ch = getchar();
    while (isdigit(ch)) n = n * 10 + ch - '0', ch = getchar();
    return n;
}

const int maxn = 100000 + 3, maxMod = 10000;
int n, m, modu, vis[maxn], cnt;
bool inCircle[maxMod];

void dfs(int x) {
    if (vis[x] == cnt) {
        int now = x;
        do {
            inCircle[now] = true;
            (now *= now) %= modu;
        } while (now != x);
        return;
    }
    vis[x] = cnt;
    dfs(x * x % modu);
}

namespace segment_tree {
    const int maxNode = (1 << 17) * 2 + 3;
    int s[maxNode], cir_cnt[maxNode], give_cnt[maxNode];
    vector<int> cir[maxNode];
    #define ls (((o) << 1) + 1)
    #define rs (((o) << 1) + 2)
    #define mid (((l) + (r)) >> 1)
    inline void push_up(int o) {
        int ls = (((o) << 1) + 1), rs = ls + 1;
        cir[o].clear(), cir_cnt[o] = 0, give_cnt[o] = 0, s[o] = s[ls] + s[rs];
        if (cir[ls].size() && cir[rs].size()) { 
            int l1 = cir[ls].size(), l2 = cir[rs].size(), l = l1 * l2 / __gcd(l1, l2);
            for (int i = 0; i < l; ++i) cir[o].push_back(cir[ls][(i + cir_cnt[ls]) % l1] + cir[rs][(i + cir_cnt[rs]) % l2]);
        }
    }
    inline void maintain(int o) {
        if (inCircle[s[o]]) {
            int now = s[o];
            do {
                cir[o].push_back(now);
                (now *= now) %= modu;
            } while (now != s[o]);
        }
    }
    inline void give_tag(int o, int t = 1) {
        (cir_cnt[o] += t) %= cir[o].size();
        (give_cnt[o] += t) %= cir[o].size();
        s[o] = cir[o][cir_cnt[o]];
    }
    inline void push_down(int o) {
        if (give_cnt[o]) give_tag(ls, give_cnt[o]), give_tag(rs, give_cnt[o]), give_cnt[o] = 0;
    }
    void build(int o, int l, int r) {
        if (r - l < 1) return;
        if (r - l == 1) maintain((s[o] = ReadInt(), o));
        else build(ls, l, mid), build(rs, mid, r), push_up(o);
    }
    void modify(int o, int l, int r, int a, int b) {
        if (l >= a && r <= b && cir[o].size()) return give_tag(o);
        if (r - l == 1) maintain(((s[o] *= s[o]) %= modu, o));
        else {
            push_down(o);
            if (mid > a) modify(ls, l, mid, a, b);
            if (mid < b) modify(rs, mid, r, a, b);
            push_up(o); //无论如何，都要重建这个环，不然标记是没办法打的！
        }
    }
    int query(int o, int l, int r, int a, int b) {
        if (l >= a && r <= b) return s[o];
        else {
            push_down(o);
            int ans = 0;
            if (mid > a) ans += query(ls, l, mid, a, b);
            if (mid < b) ans += query(rs, mid, r, a, b);
            return ans;
        }
    }
}

using namespace segment_tree;

int main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
#endif
    n = ReadInt(), m = ReadInt(), modu = ReadInt();
    memset(vis, -1, sizeof (int) * modu);
    for (int i = 0; i < modu; ++i) if (vis[i] == -1) dfs(cnt = i);
    build(0, 0, n);
    while (m--) {
        int op = ReadInt(), l = ReadInt() - 1, r = ReadInt();
        if (op == 0) modify(0, 0, n, l, r);
        else if (op == 1) printf("%d\n", query(0, 0, n, l, r));
        else assert(false);
    }
    return 0;
}
Codeforces 679B - Bear and Tower of Cubes