NOIP 2015 Day 2 详细题解

Published on 2015-11-22

感觉网上的题解很不全，只有只言片语，零零散散的，于是自己写了一份。
如果题目有些遗忘了，最好回忆一下题目再看题解。有些题目的解很可能不是最优的，欢迎各路神犇留言。

跳石子

题目地址

描述

一年一度的“跳石头”比赛又要开始了！
这项比赛将在一条笔直的河道中进行，河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间，有 NN 块岩石（不含起点和终点的岩石）。在比赛过程中，选手们将从起点出发，每一步跳向相邻的岩石，直至到达终点。
为了提高比赛难度，组委会计划移走一些岩石，使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制，组委会至多从起点和终点之间移走 MM 块岩石（不能移走起点和终点的岩石）。

提示

n,m≤50000 n, m \le 50000

分析

主要考察二分搜索以及贪心的思想。
之前的二分搜索专题本来要说这个题的，结果太懒没完结那个专题。
这是一个最大化最小值问题，可以二分答案。首先在起点和终点放一块石头。
使 C(d) C(d) 表示是否可以安排石头的位置使得最近的两头石头的距离不小于 d d 。
问题就变为求满足 C(d) C(d) 最大的 d d 。由贪心可以知道在满足条件的情况下，两个石头尽量靠近，运用贪心的思想删除石头 C(d) C(d) 。到了最后，如果当前可以删除的石头数量大于等于 00 那么就成立，否则就不成立。

代码

//  Created by Sengxian on 11/21/15.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  二分+贪心
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = 50000 + 10;
typedef long long ll;
int L, n, m;
int pos[maxn];

bool C(int d) {
    int leftS = m, lastPos = 0;
    for(int i = 1; i < n; ++i)
        if(pos[i] - pos[lastPos] < d) leftS--;
        else lastPos = i;
    return leftS >= 0;
}

void solve() {
    int lb = 0, ub = L + 10;
    while(ub - lb > 1) {
        int mid = (lb + ub) / 2;
        if(C(mid)) lb = mid;
        else ub = mid;
    }
    printf("%d\n", lb);
}

int main() {
    scanf("%d%d%d", &L, &n, &m);
    pos[0] = 0;
    for(int i = 1; i <= n; ++i)
        scanf("%d", &pos[i]);
    pos[n + 1] = L;
    n += 2;
    solve();
    return 0;
}

题外话

其实官方的数据好弱，要我出数据的我可以卡掉一批人。如果有 N=M N = M ，那么最大距离肯定就是 L L ，但是根据刚才贪心的思想，当前的 d>L2 d > \frac{L}{2} 时，如果在中间某处放置了一块石头，那么这块石头到终点就不能满足距离大于 d d 了。而且，不仅仅只有 N=M N = M 时，在其他的一些情况也可能这样。
所以，我们判断的依据必须是最后剩余可删除的石头数量，而不是最后一块石头到终点是否距离大于 dd。

子串

题目地址

描述

有两个仅包含小写英文字母的字符串 AA 和 BB。
现在要从字符串 AA 中取出 kk 个互不重叠的非空子串，然后把这 kk 个子串按照其在字符串 AA 中出现的顺序依次连接起来得到一个新的字符串。请问有多少种方案可以使得这个新串与字符串 BB 相等？
注意：子串取出的位置不同也认为是不同的方案。

提示

n≤1000,m≤200 n \le 1000, m \le 200

分析

主要考察动态规划的思想。
设 f[i][j][k]f[i][j][k] 为串 AA 匹配到第 i−1i - 1 个位置（位置从 00 开始），串 BB 匹配到 j−1j - 1 个位置，而且恰好选串 AA 的 i−1i - 1 号字符的方案总数。
设 s[i][j][k]s[i][j][k] 为串 AA 匹配到第 i−1i - 1 个位置（位置从 00 开始），串 BB 匹配到 j−1j - 1 个位置，的方案总数。可以知道 s[m][n][k]s[m][n][k] 就是要求的答案。
考虑边界，空空相对，00 组有一种方法，所以有 s[i][0][0]=1s[i][0][0] = 1。
接下来考虑状态转移方程：s[i][j][k]s[i][j][k] 是很容易求出来的。

s[i][j][k]=s[i−1][j][k]+f[i][j][k] s[i][j][k] = s[i-1][j][k] + f[i][j][k]

很好理解，s[i][j][k]s[i][j][k] 的方案数目就等于上一个阶段（串 AA 还没有使用第 i−1i - 1 个位置） 的方案数目，加上串 AA 使用第 i−1i - 1 个位置的方案总数。
怎么求解 f[i][j][k]f[i][j][k] 呢？这里运用了类似的最长公共子序列的思想。
如果 A[i−1]=B[j−1]A[i-1] = B[j-1]，那么串 AA 的 i−1i - 1 位置就可以跟 i−2i - 2 位置合成一组（如果可能的话），这时组数不变；也可以不跟 i−2i - 2 位置合成一组，自成一组，这时组数＋1。所以

f[i][j][k]=f[i−1][j−1][k]+s[i−1][j−1][k−1](A[i−1]=B[j−1]) f[i][j][k] = f[i-1][j-1][k] + s[i-1][j-1][k-1]\quad(A[i-1] = B[j-1])

如果 呢？根据定义，f[i][j][k]f[i][j][k] 要恰好选串 AA 的 i−1i - 1 号字符，现在选不了，自然为 00。所以

f[i][j][k]=0 f[i][j][k] = 0

综上所述，得到完整的状态转移方程：

最后数组压到二维的就可以省空间了。

代码

这是不压二维的版本，虽然会爆内存，但为了防止三维转二维的某些细节造成困扰，还是发出来。

//  Created by Sengxian on 11/21/15.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  DP
#include <algorithm>
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 1000 + 5, maxm = 200 + 5, moder = 1000000007;
int m, n, K;
char stra[maxn], strb[maxm];
int f[maxn][maxm][maxm], s[maxn][maxm][maxm];

void solve() {
    s[0][0][0] = 1;
    for(int i = 1; i <= n; ++i) {
        s[i][0][0] = 1; //注意如果不压到二维，这是需要的
        for(int j = 1; j <= m; ++j)
            if(stra[i-1] == strb[j-1]) {
                for(int k = 1; k <= min(K, j); ++k) {
                    f[i][j][k] = (s[i-1][j-1][k-1] + f[i-1][j-1][k]) % moder,
                    s[i][j][k] = (s[i-1][j][k] + f[i][j][k]) % moder;
                }
            }else for (int k = 1; k <= min(K, j); ++k) s[i][j][k] = s[i-1][j][k]; //注意如果不压到二维，这是需要的
    }
    printf("%d\n", s[n][m][K]);
}

int main() {
    scanf("%d%d%d%s%s", &n, &m, &K, stra, strb);
    solve();
    return 0;
}

压缩后

//  Created by Sengxian on 11/22/15.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  dp after zip 
#include <algorithm>
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 1000 + 5, maxm = 200 + 5, moder = 1000000007;
int m, n, K;
char stra[maxn], strb[maxm];
int f[maxm][maxm], s[maxm][maxm];

void solve() {
    s[0][0] = 1;
    for(int i = 1; i <= n; ++i) {
        for(int j = m; j > 0; --j)
            if(stra[i-1] == strb[j-1]) {
                for(int k = min(K, j); k > 0; --k) {
                    f[j][k] = (s[j-1][k-1] + f[j-1][k]) % moder,
                    s[j][k] = (s[j][k] + f[j][k]) % moder;
                }
            }else fill(f[j], f[j] + min(K, j) + 1, 0);
    }
    printf("%d\n", s[m][K]);
}

int main() {
    scanf("%d%d%d%s%s", &n, &m, &K, stra, strb);
    solve();
    return 0;
}

旅行计划

题目地址

描述

公元 2044 年，人类进入了宇宙纪元。
L 国有 nn 个星球，还有 条双向航道，每条航道建立在两个星球之间，这 条航道连通了 LL 国的所有星球。
小 P 掌管一家物流公司， 该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从 uiu_{i} 号星球沿最快的宇航路径飞行到 viv_{i} 号星球去。显然，飞船驶过一条航道是需要时间的，对于航道 jj，任意飞船驶过它所花费的时间为 tjt_{j}，并且任意两艘飞船之间不会产生任何干扰。
为了鼓励科技创新，L 国国王同意小 P 的物流公司参与L国的航道建设，即允许小 P 把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。
在虫洞的建设完成前小 P 的物流公司就预接了 mm 个运输计划。在虫洞建设完成后，这 mm 个运输计划会同时开始，所有飞船一起出发。当这 mm 个运输计划都完成时，小 P 的物流公司的阶段性工作就完成了。
如果小 P 可以自由选择将哪一条航道改造成虫洞，试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少？

提示

n,m≤300000 n, m \le 300000

分析

主要考察二分查找、树上倍增、贪心、“树上前缀和”。
题目是一颗树，要求将一条边的权值变为 00，使得所有运输计划的最大时间最小。
直觉告诉我们，这是一个树上倍增的题目，但是它却不像前几年的 Day2 T3 开车旅行那样纯倍增，或许更像疫情控制一些，倍增只是辅助算法，还需要配合其他算法。
由于要使所有运输计划的最大时间最小，不难想到二分答案的方法。
使 C(t) C(t) 表示是否可以改造一条边，使得改造之后所有运输计划中最长的时间不大于 t t 。这是惯用伎俩，用二分的的话，我们就可以确定一个变量 tt，正因为有了这个 tt，我们才能有的放矢的进行贪心或是干别的。
如何判断 C(t) C(t) 呢？在开始的时候用倍增预处理出所有计划的时间，如果小于等于 tt，就可以忽略，如果大于 tt，那么就要考虑在其路径上改造一条边。
由于所有时间大于 tt 的计划都要改造一条边，问题就变为了求所有时间大于 tt 的计划的路径交集，改造其中一条最大的边，看看去掉这条边之后，是否可以满足条件。
问题来了，如何求交集呢？
这里给出两种方法，一种是模拟求交集。一种是利用树上前缀和求交集。

方法一

对于两条路径来说，记它们的起始点分别为 a,b,c,da, b, c, d，则它们路径的交集的两个端点只有可能在六个点之间，即 LCA(a,b),LCA(a,c),LCA(a,d),LCA(b,c),LCA(b,d),LCA(c,d) LCA(a, b), LCA(a, c), LCA(a, d), LCA(b, c), LCA(b, d), LCA(c, d)，我们可以枚举其中两个点，看这条路径是否在都两条路径之中，而且这条路径要尽可能的长。


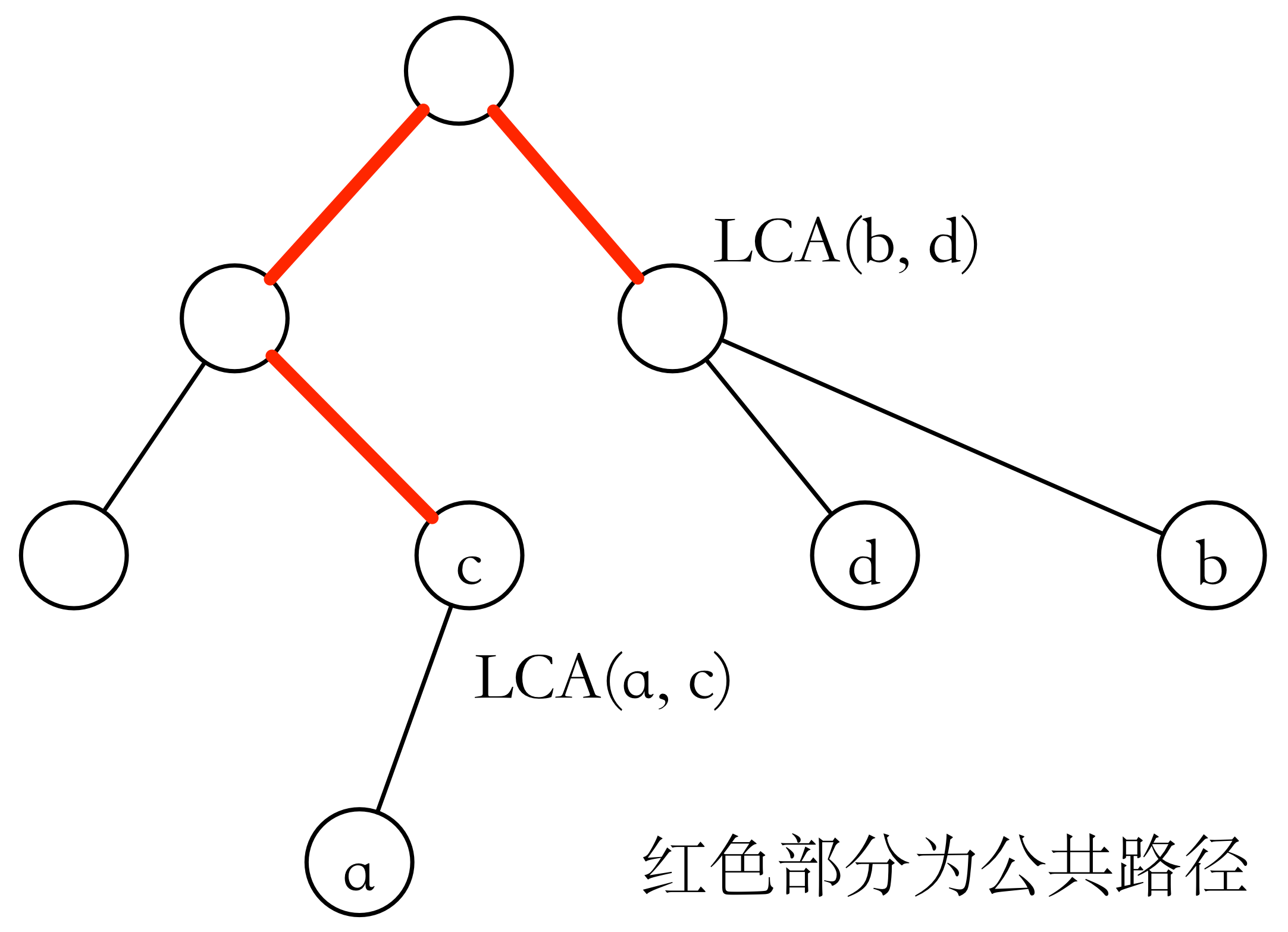
最后所有边按上面的方法顺次求交集就可以了，细节见代码一。

方法二

如果设 totaltotal 为超出时间 tt 的方案数量，边 eie_{i} 经过的次数 cnticnt_{i}。对于每个超出时间 tt 的方案，将其路径中边的 cntcnt 加 11。最后，所有 cnti=totalcnt_{i} = total 的边就是我们要求的的交集。
然而每次给每条边加一肯定是不现实的，所以我们要想出一个高效的方法，来维护边被经过的次数。
这个方法像极了2012年NOIP的 借教室 ，不过是树上的版本。我们先看看借教室的怎么处理区间加减的。
如果要对一段连续区间 [a,b)[a, b) 同时加上一个值，只需在开始处加上这个值，在结束后减去这个值，维护前缀和就行了。看上去应该是这样的：

若初始都是 00，让连续区间 [a,b)[a, b) 同时加上一个值 mm 之后，前缀和 Si=∑0iviS_{i} = \sum_0^iv_i 即为元素 ii 的值。下面是前缀和：

如果有多组加减，也不会冲突。
同样的，在树上，我们用 sis_i 来表示顶点 ii 到其父亲的这条边被经过的次数，viv_i 用于记录顶点信息。
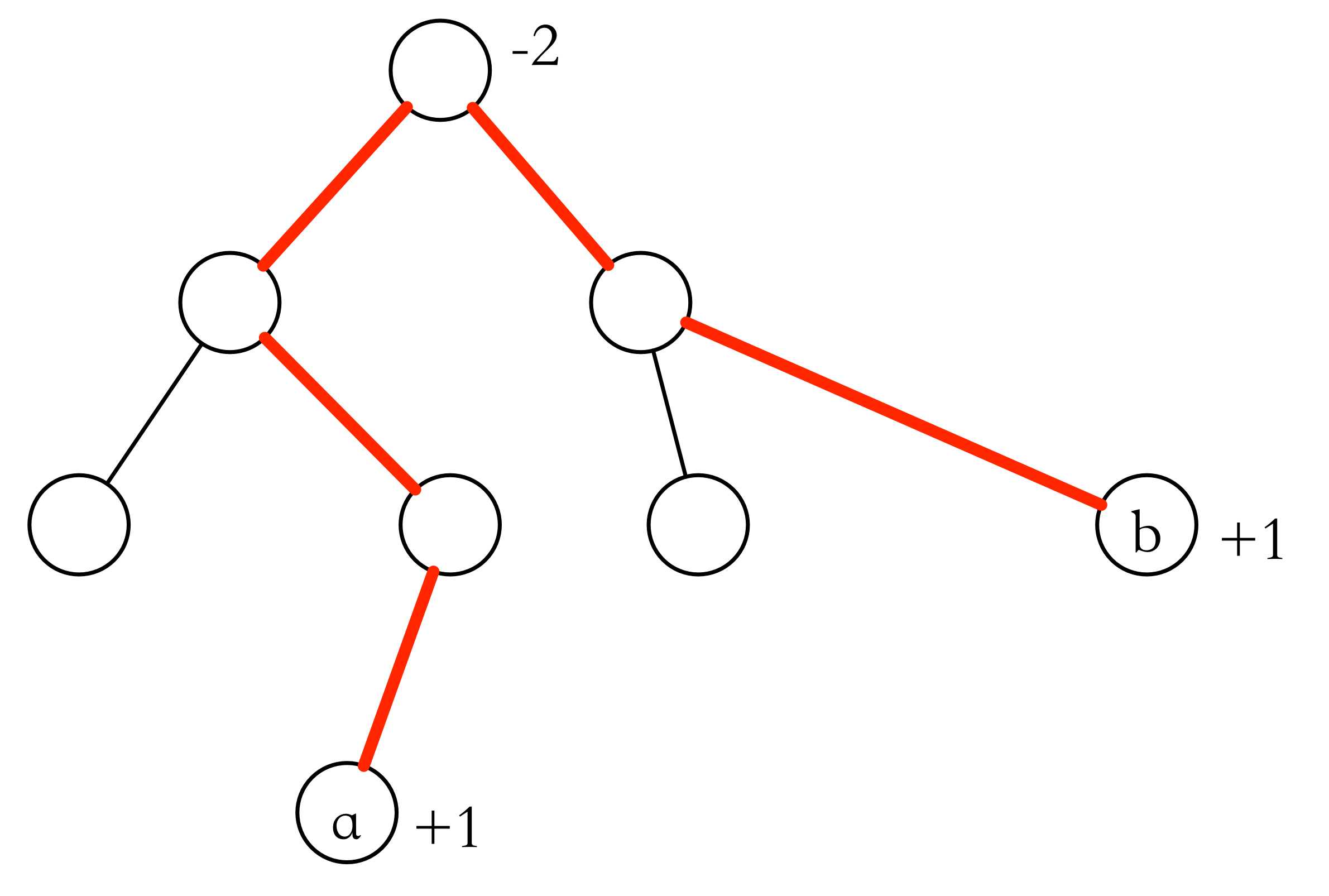
对于每个点对 (a,b)(a, b)，我们将 va+1,vb+1,vLCA(a,b)−2v_a + 1, v_b + 1, v_{LCA(a, b)} - 2。


则树上前缀和 si=∑k∈son(i)vks_{i} = \sum\limits_{k \in son(i)}{v_k}。


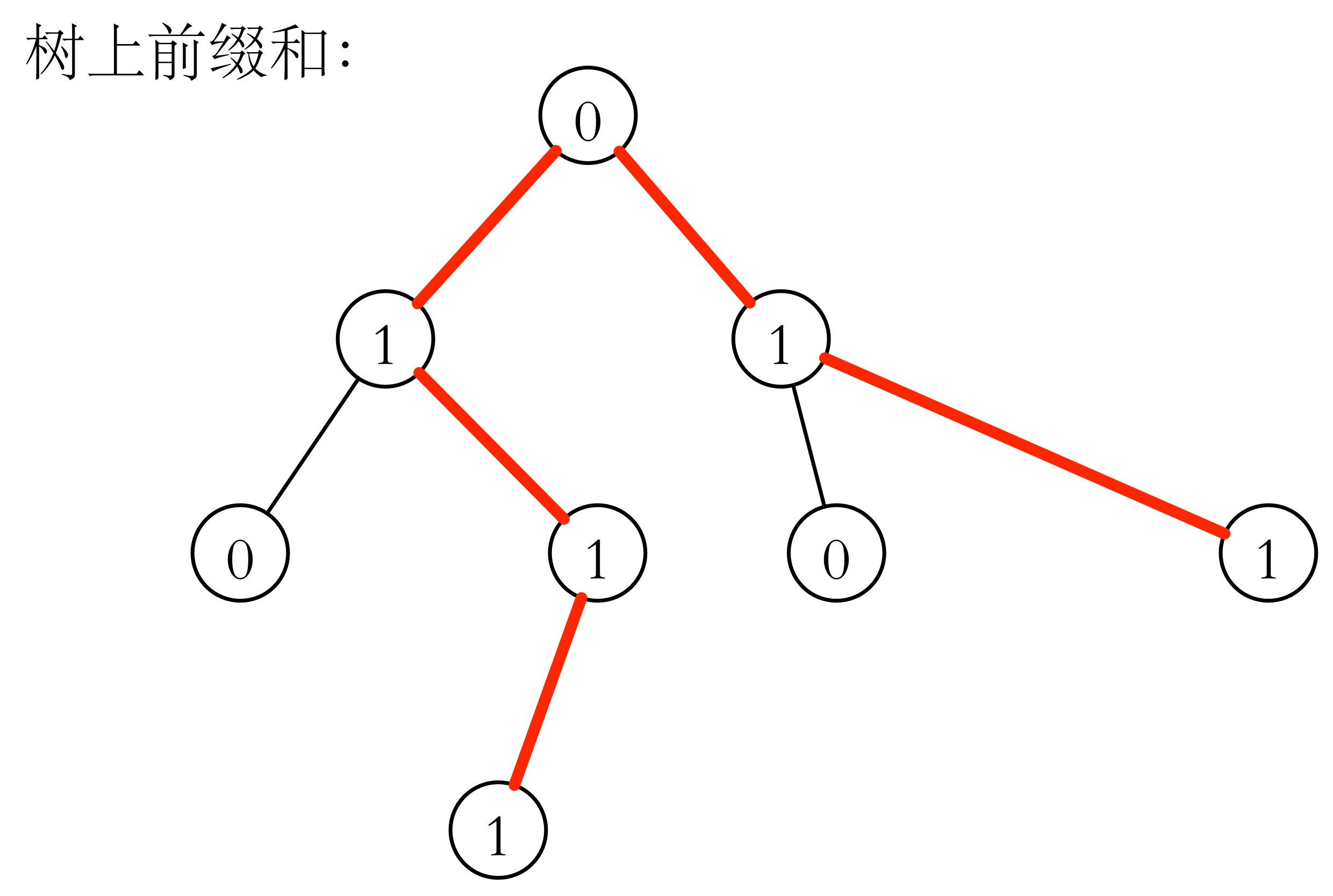
利用 dfsdfs 序，对于每个点更新它的父亲的 ss 值，前缀和可以在 O(n)O(n) 的时间内算出来。这样，每条边经过的次数就顺利计算出来了。
这个方法的复杂度是线性的，为 O(m+n)O(m+n)。

代码

方法一：

//  Created by Sengxian on 11/21/15.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  模拟求交集
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int maxn = 300000 + 5, INF = 1000000000;
int n, m;
struct edge {
    int to, cost;
}es[maxn * 2];
int first[maxn], nextE[maxn * 2];
int qf[maxn], qt[maxn], qcost[maxn];
int depth[maxn], ancestor[maxn][20], costs[maxn][20], maxCost[maxn][20];

inline int ReadInt() {
    char ch = getchar();
    int n = 0;
    while(ch < '0' || ch > '9')
        ch = getchar();
    do {
        n = (n << 1) + (n << 3) + ch - '0';
        ch = getchar();
    }while(ch >= '0' && ch <= '9');
    return n;
}

int etmp = 0;
inline void addEdge(int f, int t, int c) {
    es[etmp].to = t;
    es[etmp].cost = c;
    nextE[etmp] = first[f];
    first[f] = etmp;
    etmp++;
}

void dfs(int cur, int fa) {
    depth[cur] = fa == -1 ? 0 : depth[fa] + 1;
    ancestor[cur][0] = fa;
    for(int q = first[cur]; q != -1; q = nextE[q]) {
        int v = es[q].to;
        if(v != fa) {
            maxCost[v][0] = costs[v][0] = es[q].cost;
            dfs(v, cur);
        }
    }
}

int allCost, maxC, lca;
void Query(int a, int b) {
    if(depth[a] < depth[b]) swap(a, b);
    int bits = 0, q = 1;
    while(depth[a] - q > 0) bits++, q *= 2;
    allCost = maxC = lca = 0;
    for(int i = bits; i >= 0; --i)
        if(depth[a] - (1 << i) >= depth[b]) {
            allCost += costs[a][i];
            maxC = max(maxC, maxCost[a][i]);
            a = ancestor[a][i];
        }
    if(a == b) {
        lca = a;
        return;
    }
    for(int i = bits; i >= 0; --i)
        if((depth[a] - (1 << i) >= 0) && ancestor[a][i] != ancestor[b][i]) {
            allCost += costs[a][i] + costs[b][i];
            maxC = max(maxC, max(maxCost[a][i], maxCost[b][i]));
            a = ancestor[a][i];
            b = ancestor[b][i];
        }
    allCost += costs[a][0] + costs[b][0];
    maxC = max(maxC, max(maxCost[a][0], maxCost[b][0]));
    lca = ancestor[a][0];
}

void process() {
    dfs(0, -1);
    for(int w = 1; (1 << w) < n; ++w)
        for(int i = 0; i < n; ++i)
            if(depth[i] - (1 << w) >= 0)
                ancestor[i][w] = ancestor[ancestor[i][w-1]][w-1],
                costs[i][w] = costs[i][w-1] + costs[ancestor[i][w-1]][w-1],
                maxCost[i][w] = max(maxCost[i][w-1], maxCost[ancestor[i][w-1]][w-1]);
    for(int i = 0; i < m; ++i) {
        Query(qf[i], qt[i]);
        qcost[i] = allCost;
    }
}

inline int Lca(int a, int b) {
    Query(a, b);
    return lca;
}

inline int Length(int a, int b) {
    Query(a, b);
    return allCost;
}

inline int MaxC(int a, int b) {
    Query(a, b);
    return maxC;
}

//is path(a, b) in path(f, t)
inline int inPath(int f, int t, int a, int b) {
    //consider f - t is longer than a - b
    int len1 = Length(a, f), len2 = Length(b, f);
    if(len2 < len1) {
        swap(a, b); len1 = len2;
    }
    int len3 = Length(a, b);
    return (len1 + Length(b, t) + len3) == Length(f, t) ? len3 : 0;
}

//get the intersection of path(a, b) and path(c, d) 's length
inline int Getintersection(int &a, int &b, int c, int d) {
    int _a = -1, _b = -1, nowLength = 0;
    vector<int> k;
    k.push_back(Lca(a, b));
    k.push_back(Lca(a, c));
    k.push_back(Lca(a, d));
    k.push_back(Lca(b, c));
    k.push_back(Lca(b, d));
    k.push_back(Lca(c, d));
    k.erase(unique(k.begin(), k.end()), k.end());
    for(unsigned int i = 0; i < k.size(); ++i)
        for(unsigned int j = i + 1; j < k.size(); ++j) {
            int l = inPath(a, b, k[i], k[j]);
            if(l > nowLength && inPath(c, d, k[i], k[j])) {
                _a = k[i], _b = k[j], nowLength = l;
            }
        }    
    a = _a, b = _b;
    return nowLength;
}

bool C(int t) {
    int a = -1, b = -1;
    for(int i = 0; i < m; ++i) {
        if(qcost[i] <= t) continue;
        if(a == -1 && b == -1)
            a = qf[i], b = qt[i];
        else if(Getintersection(a, b, qf[i], qt[i]) <= 0)
            return false;
    }
    int dec = MaxC(a, b);
    for(int i = 0; i < m; ++i)
        if(qcost[i] - dec > t)
            return false;
    return true;
}

void solve() {
    int lb = -1, ub = INF;
    while(ub - lb > 1) {
        int mid = (lb + ub) / 2;
        if(C(mid)) ub = mid;
        else lb = mid;
    }
    printf("%d\n", ub);
}

int main() {
    n = ReadInt(), m = ReadInt();
    fill(first, first + n, -1);
    for(int i = 0; i < n - 1; ++i) {
        int f = ReadInt() - 1, t = ReadInt() - 1, c = ReadInt();
        addEdge(f, t, c);
        addEdge(t, f, c);
    }
    for(int i = 0; i < m; ++i)
        qf[i] = ReadInt() - 1, qt[i] = ReadInt() - 1;
    process();
    solve();
    return 0;
}

代码二（用到了非递归）：

//  Created by Sengxian on 11/21/15.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  树上前缀和 + LCA
#include <bits/stdc++.h>
using namespace std;

inline int ReadInt() {
    static int n, ch;
    n = 0, ch = getchar();
    while (!isdigit(ch)) ch = getchar();
    while (isdigit(ch)) n = n * 10 + ch - '0', ch = getchar();
    return n;
}

const int MAX_N = 300000 + 3, MAX_M = 300000 + 3, INF = 0x3f3f3f3f;
struct edge {
    edge *next;
    int to, cost;
    edge(edge *next = NULL, int to = 0, int cost = 0): next(next), to(to), cost(cost) {}
} pool[MAX_N * 2], *pit = pool, *first[MAX_N];
int n, m;
int query_from[MAX_M], query_to[MAX_M], query_cost[MAX_M], query_lca[MAX_M];
int depth[MAX_N], dis[MAX_N], fc[MAX_N], ancestor[20][MAX_N];

int dfsSeq[MAX_N], cnt = 0;
void dfs() {
    static int stk[MAX_N];
    static bool vis[MAX_N];
    memset(vis, 0, sizeof (bool) * n);
    int sz = 0;
    stk[sz++] = 0;
    ancestor[0][0] = -1, depth[0] = 0, dis[0] = 0;
    while (sz) {
        int u = stk[sz - 1];
        if (!vis[u]) {
            for (const edge *e = first[u]; e; e = e->next) {
                if (e->to != ancestor[0][u]) {
                    depth[e->to] = depth[u] + 1;
                    dis[e->to] = dis[u] + e->cost;
                    fc[e->to] = e->cost;
                    ancestor[0][e->to] = u;
                    stk[sz++] = e->to;
                }
            }
            vis[u] = true;
        } else dfsSeq[cnt++] = stk[--sz];
    }
}

int work(int a, int b) {
    if (depth[a] < depth[b]) swap(a, b);
    int bits = 0, q = 1;
    while (depth[a] - q > 0) bits++, q <<= 1;
    for (int i = bits; i >= 0; --i)
        if (depth[a] - (1 << i) >= depth[b])
            a = ancestor[i][a];
    if (a == b) return a;
    for (int i = bits; i >= 0; --i)
        if ((depth[a] - (1 << i) >= 0) && ancestor[i][a] != ancestor[i][b])
            a = ancestor[i][a], b = ancestor[i][b];
    return ancestor[0][a];
}

void process() {
    dfs();
    for (int w = 1; (1 << w) < n; ++w)
        for (int i = 0; i < n; ++i)
            if (depth[i] - (1 << w) >= 0)
                ancestor[w][i] = ancestor[w - 1][ancestor[w - 1][i]];
    for (int i = 0; i < m; ++i) {
        int LCA = work(query_from[i], query_to[i]);
        query_cost[i] = dis[query_from[i]] + dis[query_to[i]] - 2 * dis[LCA];
        query_lca[i] = LCA;
    }
}

int s[MAX_N];
bool C(int t) {
    int total = 0, maxT = 0;
    memset(s, 0, sizeof (int) * n);
    for (int i = 0; i < m; ++i) {
        if (query_cost[i] <= t) continue;
        total++;
        s[query_from[i]]++, s[query_to[i]]++, s[query_lca[i]] -= 2;
        maxT = max(maxT, query_cost[i] - t);
    }
    for (int i = 0, u; i < n; ++i) {
        u = dfsSeq[i];
        s[ancestor[0][u]] += s[u];
    }
    int dec = 0;
    for (int i = 0; i < n; ++i)
        if (s[i] == total) dec = max(dec, fc[i]);
    return maxT <= dec;
}

void solve() {
    int l = -1, r = 300000000;
    while (r - l > 1) {
        int mid = (l + r) >> 1;
        if (C(mid)) r = mid;
        else l = mid;
    }
    printf("%d\n", r);
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
#endif
    n = ReadInt(), m = ReadInt();    
    for (int i = 0, f, t, c; i < n - 1; ++i) {
        f = ReadInt() - 1, t = ReadInt() - 1, c = ReadInt();
        first[f] = new(pit++) edge(first[f], t, c);
        first[t] = new(pit++) edge(first[t], f, c);
    }
    for(int i = 0; i < m; ++i)
        query_from[i] = ReadInt() - 1, query_to[i] = ReadInt() - 1;
    process();
    solve();
    return 0;
}
UVa 257 - Palinwords