QTREE 1 - Query on a tree I

#树链剖分 #QTREE
Published on 2016-03-16

题目地址
开始打 QTREE 系列。

描述

给你一个 n(n≤10000)n(n\le 10000) 个节点的树， 现在要你支持两种操作：

  • QUERY a b 询问 aa 到 bb 的路径上的最大边权。
  • CHANGE i ti 修改第 ii 条边的权值为 tit_i。

分析

考虑树链剖分。
树链剖分的准备工作。首先无根树转有根树，以 11 为根，记录每个节点的子节点总数（包括自己） ss，每个节点的父亲 fafa，每个节点到父亲的边权 fvfv，深度 depdep。这是第一次 dfs。
开始树链剖分，其实很简单，将一棵树，转换为链状结构，每一条链，都是一棵线段树，线段树节点的值表示对应节点到其父亲的边权，节点 1 到父亲的边权为 0。见下图，剖分的实质就是把树形结构转换为容易处理的线性结构。

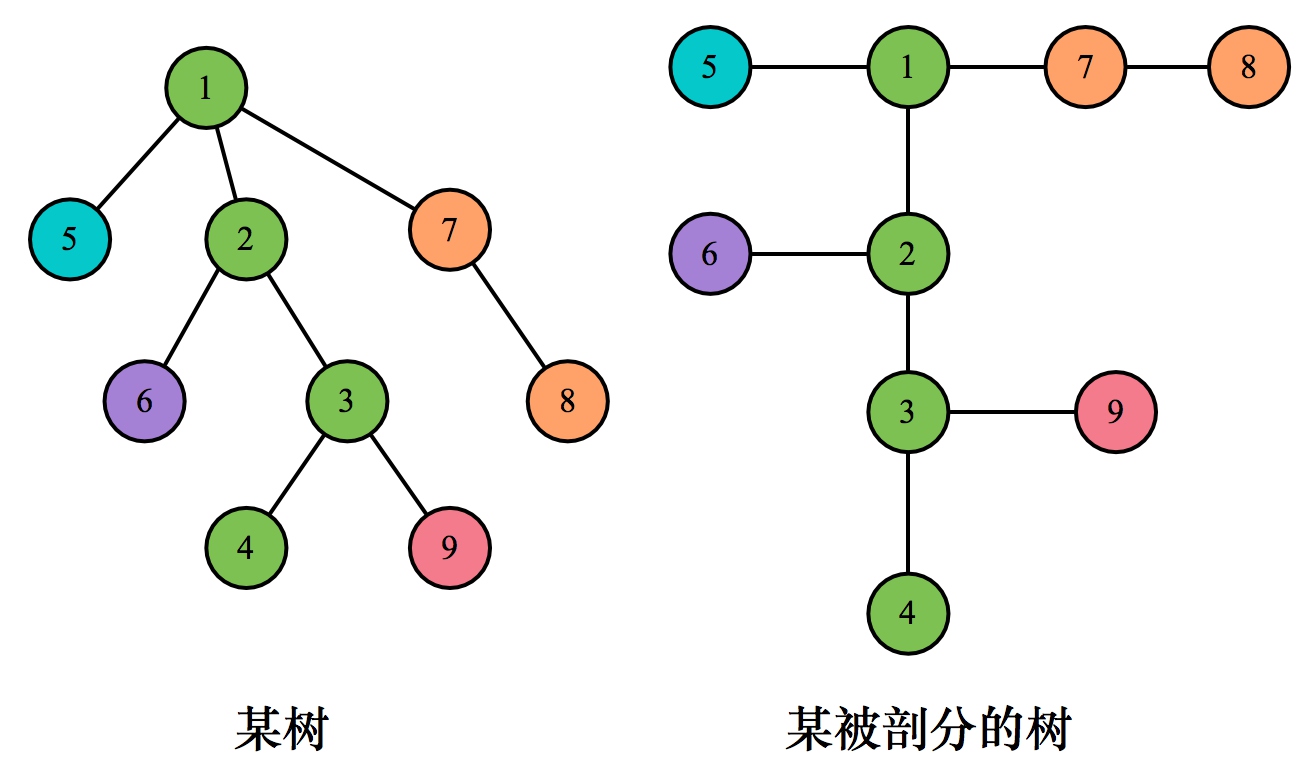
为了保证时间复杂度，我们在建立链的时候，要有所选择。第二次 dfs：得到每个节点所在链的头节点 belbel，每个节点的 dfs 序编号 idid。
dfs 的过程是这样的，首先维护一个时间戳 timestamp\text{timestamp}，dfs(int u, int num) 表示从节点 uu 开始构建链，节点 uu 属于链编号 numnum。dfs 进来的时候，每个节点的 id=timestamp++id = \text{timestamp++}，使用 dfs 序作为标号的原因是为了保证相同的链中的节点的 id 连续，使得我们可以只需要维护一棵线段树。
然后找到 uu 儿子中 ss 最大的节点 vv（若没有，则为叶子，返回），执行 dfs(v, num) 这是为了使这一条链尽可能的长，保证时间复杂度。然后其余的儿子节点构成新链，自己就是新链的表头，执行 dfs(son, son)。
接着构建线段树，由于同一个链的所有节点标号连续，所以可以在一棵线段树里面搞定，使用 id[v]id[v] 作为节点 vv 在线段树里面的位置，线段树节点的值是节点到其父亲的距离。
怎么修改呢？就是个裸的单点修改，没有难度。
怎么查询 aa 到 bb 的距离呢？显然我们要跨过很多链，最终使得它们在同一条链上面。
首先通过交换，保证 aa 所在链的头结点的深度大于 bb 所在链的头结点的深度（这很像向上爬的过程，显然应该从深度大的向上爬，就像 LCA），然后将 aa 移动到 fa[bel[a]]fa[bel[a]] 即上一条链，更新最大边权。
不断执行这个过程，直到 bel[a]=bel[b]bel[a] = bel[b]，再在这一条链上执行一次区间最大值。答案就出来了！
单次操作复杂度 O(log2n)O(\log^2n)。
细节见代码。

代码

//  Created by Sengxian on 3/16/16.
//  Copyright (c) 2016年 Sengxian. All rights reserved.
//    Spoj QTREE I
#include <algorithm>
#include <iostream>
#include <climits>
#include <cctype>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <vector>
using namespace std;

inline int ReadInt() {
    int n = 0, ch = getchar(); bool flag = false;
    while (!isdigit(ch)) flag |= ch == '-', ch = getchar();
    while (isdigit(ch)) n = (n << 1) + (n << 3) + ch - '0', ch = getchar();
    return flag ? -n : n;
}

struct SegmentTree {
    static const int maxNode = (1 << 14) * 2 + 100;
    int *v, n, realN, maxValue[maxNode];
    int buildTree(int k, int l, int r) {
        if (l >= r) return INT_MIN;
        if (r - l == 1) return maxValue[k] = l < realN ? v[l] : INT_MIN;
        else return maxValue[k] = max(buildTree(k * 2 + 1, l, (l + r) / 2), buildTree(k * 2 + 2, (l + r) / 2, r));
    }
    void build(int _n, int *_v) {
        n = 1, realN = _n, v = _v;
        while (n < _n) n <<= 1;
        buildTree(0, 0, n);
    }
    void modify(int k, int v) {
        k += n - 1;
        maxValue[k] = v;
        while (k > 0) {
            k = (k - 1) / 2;
            maxValue[k] = max(maxValue[k * 2 + 1], maxValue[k * 2 + 2]);
        }
    }
    int a, b;
    int query(int k, int l, int r) {
        if (r <= a || l >= b) return INT_MIN;
        else if(l >= a && r <= b) return maxValue[k];
        return max(query(k * 2 + 1, l, (l + r) / 2), query(k * 2 + 2, (l + r) / 2, r));
    }
    int MaxValue(int _a, int _b) {
        a = _a, b = _b;
        return query(0, 0, n);
    }
}Seg;

const int maxn = 10000 + 3;
struct edge {
    int from, to, cost;
    inline int To(int f) {
        if(f == from) return to;
        else return from;
    }
    edge(int from, int to, int cost): from(from), to(to), cost(cost) {}
};
vector<edge> Edges;
vector<int> G[maxn];
int n, s[maxn], fa[maxn], fv[maxn], dep[maxn], id[maxn], bel[maxn], timestamp = 0;
//子节点数目，父亲，到父亲的边权，深度，dfs标号（在线段树中的 id），链头的编号

void init() {
    for (int i = 0; i < n; ++i) G[i].clear();
    Edges.clear();
    timestamp = 0; fa[0] = -1; fv[0] = 0;
    int f, t, c;
    for (int i = 0; i < n - 1; ++i) {
        f = ReadInt() - 1, t = ReadInt() - 1, c = ReadInt();
        Edges.push_back(edge(f, t, c));
        G[f].push_back(Edges.size() - 1);
        G[t].push_back(Edges.size() - 1);
    }
}

int dfs1(int u, int f) {
    fa[u] = f, dep[u] = u == 0 ? 0 : dep[f] + 1;
    s[u] = 1;
    for (int i = 0; i < (int)G[u].size(); ++i) {
        edge &e = Edges[G[u][i]]; int v = e.To(u);
        if (v != f) {
            fv[v] = e.cost;
            s[u] += dfs1(v, u);
        }
    }
    return s[u];
}

void dfs2(int u, int num) {
    id[u] = timestamp++;
    bel[u] = num;
    int Max = 0, idx = -1;
    for (int i = 0; i < (int)G[u].size(); ++i) {
        edge &e = Edges[G[u][i]]; int v = e.To(u);
        if (v != fa[u] && s[v] > Max) {Max = s[v], idx = v;}
    }
    if(Max == 0) return;
    dfs2(idx, num);
    for (int i = 0; i < (int)G[u].size(); ++i) {
        edge &e = Edges[G[u][i]]; int v = e.To(u);
        if (v != fa[u] && v != idx)
            dfs2(v, v);
    }
}

int v[maxn];
void build() {
    for (int i = 0; i < n; ++i)
        v[id[i]] = fv[i];
    Seg.build(n, v);
}

int query(int a, int b) {
    int maxVal = INT_MIN;
    while (bel[a] != bel[b]) {
        if (dep[bel[a]] < dep[bel[b]]) swap(a, b);
        maxVal = max(maxVal, Seg.MaxValue(id[bel[a]], id[a] + 1));
        a = fa[bel[a]];
    }
    if (a == b) return maxVal;
    if (dep[a] < dep[b]) swap(a, b);
    maxVal = max(maxVal, Seg.MaxValue(id[b] + 1, id[a] + 1)); //注意是 +1
    return maxVal;
}

char op[10];
int main() {
    int caseNum = ReadInt();
    while (caseNum--) {
        n = ReadInt();
        init();
        dfs1(0, -1); //第一次dfs
        dfs2(0, 0);  //第二次dfs
        build();
        while (scanf("%s", op) && op[0] != 'D') {
            if (op[0] == 'C') {
                int i = ReadInt() - 1, c = ReadInt();
                int f = Edges[i].from, t = Edges[i].to;
                if(dep[t] > dep[f]) {
                    Seg.modify(id[t], c); //改的是 id
                }else Seg.modify(id[f], c);
            }else if (op[0] == 'Q') printf("%d\n", query(ReadInt() - 1, ReadInt() - 1));
        }
        if (caseNum) putchar('\n');
    }
    return 0;
}
QTREE 2 - Query on a tree II