UVa 1327 - King's Quest | Sengxian's Blog

UVa 1327 - King's Quest

#强联通分量

Published on 2015-12-24

描述

从前有一个国王，它有 $n(n\le 2000)$ 个王子。皇宫里面还有 $n(n\le 2000)$ 个姑娘，并且国王知道每个王子喜欢的姑娘是谁。巫师根据王子喜欢的姑娘，给出了一组可行的方案，使得每个王子都可以与自己喜欢的姑娘结婚。现在国王想知道，每个王子能娶到的姑娘的列表（即其他王子仍可以娶到自己喜欢到的姑娘）。

样例输入

样例输出

附加输入

附加输出

分析

这不是稳定婚姻问题！有配对不一定是稳定婚姻问题，稳定婚姻存在一个优先级的排序。当然可以用求婚－拒绝算法，但复杂度极高极高，甚至不如多跑几次完美匹配，TLE 无疑。

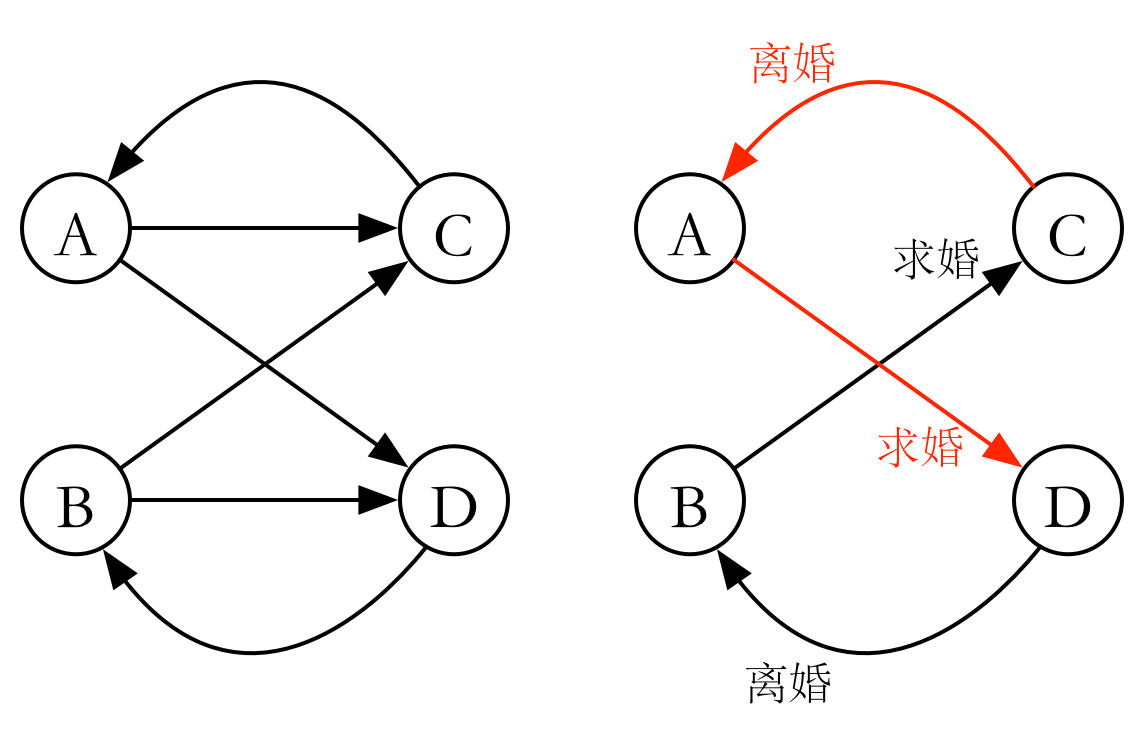
这样考虑，我们手头已经有一个完美方案了，现在有王子 $A$ ，方案中他与姑娘 $C$ 结婚。但他现在想与姑娘 $D$ 结婚，行不行呢？姑娘 $D$ 找到他的王子 $B$ ，问他能不能够与别人结婚， $B$ 恰好可以与 $C$ 结婚。于是 $A - D$ 成功结婚，怎么样，这样就形成了一个圈 $A\rightarrow D\rightarrow B\rightarrow C\rightarrow A$ 。
我们对于王子 $i$ 喜欢姑娘 $j$ ，连边 $i \rightarrow j$ 表示求婚。对于王子 $i$ 与姑娘 $j$ 结婚这一现有方案，连边 $j \rightarrow i$ 表示离婚。所以王子 $i$ 能与姑娘 $j$ 结婚当且仅当他们在一个强联通分量的时候（即能够形成上文所说的圈）。好好想一想这个求婚-离婚的过程。

代码

//  Created by Sengxian on 12/24/15.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  Uva 1327 强联通分量
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <vector>
#include <stack>
#include <numeric>
#include <queue>
using namespace std;
const int maxn = 2000 + 3, maxNode = maxn * 2;
vector<int> G[maxNode];
int n, sccno[maxNode], pre[maxNode], timestamp, scc_cnt;
stack<int> stk;

inline void tension(int &a, int b) {
    if(b < a) a = b;
}

int dfs(int u) {
    int lowu = pre[u] = ++timestamp;
    stk.push(u);
    for(int i = 0; i < G[u].size(); ++i) {
        int v = G[u][i];
        if(!pre[v]) tension(lowu, dfs(v));
        else if(!sccno[v]) tension(lowu, pre[v]); //反向边
    }
    if(lowu == pre[u]) {
        scc_cnt++;
        while(!stk.empty()) {
            int x = stk.top(); stk.pop();
            sccno[x] = scc_cnt;
            if(x == u) break;
        }
    }
    return lowu;
}

void find_scc() {
    fill(pre, pre + 2 * n, 0);
    fill(sccno, sccno + 2 * n, 0);
    timestamp = scc_cnt = 0;
    for(int i = 0; i < 2 * n; ++i)
        if(!pre[i]) dfs(i);
}

inline int ReadInt() {
    int n = 0, ch = getchar();
    while(ch < '0' || ch > '9') ch = getchar();
    do {
        n = n * 10 + ch - '0';
        ch = getchar();
    }while(ch >= '0' && ch <= '9');
    return n;
}

int main() {
    int t;
    while(~scanf("%d", &n)) {
        //0 ~ n 王子
        //n ~ 2n 女孩
        for(int i = 0; i < n; ++i) {
            G[i].clear(); G[i + n].clear(); t = ReadInt();
            while(t--) G[i].push_back(ReadInt() - 1 + n);
        }
        for(int i = 0; i < n; ++i) {
            G[ReadInt() - 1 + n].push_back(i);
        }
        find_scc();
        for(int i = 0; i < n; ++i) {
            vector<int> ans;
            for(int j = 0; j < G[i].size(); ++j)
                if(sccno[i] == sccno[G[i][j]]) ans.push_back(G[i][j] - n + 1);
            printf("%d", ans.size());
            for(int j = 0; j < ans.size(); ++j) printf(" %d", ans[j]);
            printf("\n"); 
        }
    }
    return 0;
}

UVa 10735 - Euler Circuit(混合图欧拉回路) UVa 1459 - Flowers Placement