UVa 1533 - Moving Pegs

#BFS #暴力 #状态压缩
Published on 2016-01-21

题目地址

描述

给定一个有 1515 个格子三角形状的棋盘，除了给定的一个位置 empty\mathrm{empty} 每一个位置上都有一个棋子，你可以进行移动棋子，直到棋盘只剩下最后一个棋子在位置 emptyempty，但必须遵循如下规则：

  • 你每次可以选择任意一个有棋子的格子开始移动。
  • 每次移动必须沿着直线移动，必须隔至少 11 个格子移动（例如 22 不可以移动到 55，因为中间没有间隔），但只能移动到没有棋子的格子。
  • 移动的过程中起始位置和途中经过的格子必须有棋子，移动完毕后，这些棋子会被消去（例如从 12→512 \rightarrow 5 之后，格子 12,812, 8 的棋子被消去，格子 55 有一颗棋子）。

请你输出字典序最小的移动方案。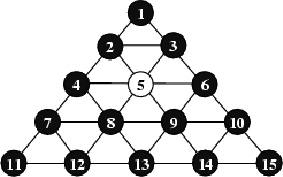

样例输入

1                                                   
5

样例输出

10
12 5 3 8 15 12 6 13 7 9 1 7 10 8 7 9 11 14 14 5

分析

题意搞清楚之后明显不难，但我根本不知道跳棋规则，样例都炸了好半天。。。
记录每一个格子的 66 个移动方向移动到的格子，由于需要字典序最小，那么依此按照左上，右上，左，右，左下，右下的顺序来保证字典序最小。
用二进制位记录格子上是否有棋子，然后 BFS + 状压判重即可。215−12 ^{15} - 1 个状态完全可行。注意 BFS 扩展的时候先从标号小的开始扩展保证字典序。
细节见代码，标号从 00 开始。当然打表这种猥琐事情我就不干了。

代码

//  Created by Sengxian on 1/21/16.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  UVa 1533 BFS
#include <algorithm>
#include <iostream>
#include <climits>
#include <cassert>
#include <cstring>
#include <cstdio>
#include <queue>
#include <cmath>
#include <vector>
#define br putchar('\n')
using namespace std;
int dir[15][6] = <!--0-->;

inline int ReadInt() {
    int x = 0, ch = getchar();
    while(!isdigit(ch)) ch = getchar();
    do {
        x = x * 10 + ch - '0';
        ch = getchar();
    }while(isdigit(ch));
    return x;
}    

const int maxn = 15;
struct state {
    int S, cnt;
    int step[maxn][2];
    state(): cnt(0) {}
    void erase(int x) {if((S >> x) & 1) S ^= 1 << x;}
    void add(int x) {if(!((S >> x) & 1)) S += 1 << x;}
    bool count(int x) {return (S >> x) & 1;}
    void print() {
        for(int i = 14; i >= 0; --i)
            printf("%d", (S >> i) & 1);
        br;
    }
    state operator = (const state &s) {
        S = s.S;
        cnt = s.cnt;
        memcpy(step, s.step, sizeof(s.step));
        return *this;
    }
}s;
bool vis[1 << maxn];

bool Solve(int empty) {
    queue<state> q;
    memset(vis, 0, sizeof(vis));
    state s; s.S = (1 << maxn) - 1; s.erase(empty);
    q.push(s);
    vis[s.S] = true;
    while(!q.empty()) {
        state now = q.front(); q.pop();
        for(int u = 0; u < maxn; ++u) {
            if(!now.count(u)) continue; //no peg so cannot move.
            for(int k = 0; k < 6; ++k) {
                state news = now;
                int v = u;
                news.erase(u);
                int tot = 0;
                while(true) {
                    v = dir[v][k];
                    tot++;
                    if(v == -1) break; //cannot go further.
                    if(news.count(v)) {news.erase(v); continue;} //cannot move to it since there are peg in it.
                    if(tot == 1) break;
                    news.add(v);
                    if(!vis[news.S]) {
                        vis[news.S] = true;
                        news.cnt = now.cnt + 1;
                        news.step[now.cnt][0] = u;
                        news.step[now.cnt][1] = v;
                        q.push(news);
                        if(news.S == (1 << empty)) {
                            printf("%d\n", news.cnt);
                            for(int i = 0; i < news.cnt; ++i)
                                printf("%d %d%c", news.step[i][0] + 1, news.step[i][1] + 1, i + 1 == news.cnt ? '\n' : ' ');
                            return true;
                        }
                    }
                    news.erase(v);
                    break;
                }
            }
        }
    }
    return false;
}

int main() {
    int caseNum = ReadInt();
    while(caseNum--) {
        int empty = ReadInt() - 1;
        if(!Solve(empty)) puts("IMPOSSIBLE");
    }
    return 0;
}

附加输入

15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

附加输出

9
4 1 6 4 11 2 14 11 15 6 1 10 10 7 11 4 4 1
9
7 2 1 4 10 1 14 2 1 7 11 14 15 13 13 4 7 2
9
10 3 1 6 7 1 12 3 1 10 14 12 11 13 13 6 15 3
9
1 4 6 1 13 6 10 3 11 13 3 12 15 11 11 2 1 4
10
12 5 3 8 15 12 6 13 7 9 1 7 10 8 7 9 11 14 14 5
9
1 6 4 1 13 4 7 2 15 13 2 14 11 15 15 3 1 6
9
1 7 6 1 11 4 9 7 14 11 11 2 15 6 6 4 1 7
10
3 8 12 5 15 3 13 6 1 10 2 9 11 2 14 5 2 9 10 8
10
2 9 11 2 12 5 3 8 13 4 1 7 14 5 15 3 3 8 7 9
9
1 10 4 1 11 4 4 6 12 5 10 8 15 12 12 3 1 10
9
4 11 1 4 10 1 14 2 1 7 11 14 15 13 13 4 4 11
9
14 12 2 14 7 2 1 4 15 13 3 15 11 14 4 13 15 12
9
4 13 1 4 11 2 13 11 15 13 2 14 3 15 15 12 11 13
9
11 14 2 11 3 12 10 3 1 6 11 13 15 12 6 13 12 14
9
6 15 1 6 7 1 12 3 1 10 15 12 11 13 13 6 6 15
UVa 812 - Trade on Verweggistan