Sengxian's Blog

介绍

现有 $n$ 个布尔变量 $x_{i}$，给出一些限制关系，比如 x1为真或者 x2 为假、x3 为真或者 x5 为真 等（注意这里的‘或’是指至少有一个条件成立），SAT 问题是要确定 $n$ 个布尔变量的值，使得其满足所有限制关系。特别的，若每种限制关系中最多只对两个元素进行限制，则称为 2-SAT 问题。我们这里讨论 2-SAT 问题。

解法

2-SAT 问题难在建模，所以一般来说不会在时间上卡你，故用一种较为简洁，较好理解的方法就可以了，不需要那么麻烦。下面给出一种算法（来自刘汝佳的训练指南）。当然，有兴趣的可以参见神犇们的论文，有线性时间复杂度的解法：

对称性解决2-sat
赵爽的2-SAT解法浅析论文

构建一张有向图 $G$,其中每个变量 $x_{i}$ 拆成两个节点 $2i$ 和 $2i + 1$，分别表示 $x_{i}$ 为假以及 $x_{i}$ 为真。在最后要为每一个变量选择其中的一个结点标记。比如，若标记了节点 $2i$，则表示 $x_{i}$ 为假；若标记了节点 $2i+1$，则表示 $x_{i}$ 为真。
对于 xi 为假或者 xj 为假 这样的条件，我们连一条有向边 $2i + 1 \rightarrow 2j$，表示如果标记节点 $2i+1$，那么也必须标记节点 $2j$（因为如果 $x_{i}$ 为真，则 $x_{j}$ 必须为假才能使条件成立）。这条有向边相当于"推导出"的意思。同理，还需要连接一条有向边 $2j + 1 \rightarrow 2i$。对于其他情况，也可以类似连边。换句话说，每个条件对应两条“对称”的边。
接下来逐一考虑没有标记的变量，设为 $x_{i}$。我们先假定它为假，然后标记节点 $2i$，并且沿着有向边标记所有能标记的节点。如果标记过程中发现某个变量所对应的两个节点都被标记了，则 " $x_{i}$ 为假" 这个假定不成立，需要改成 " $x_{i}$ 为真"，然后退回到标记 " $x_{i}$ 为假" 之前的状态，重新操作。注意，如果当前考虑的变量不管是真是假都会引起矛盾，可以证明整个 2-SAT 问题无解（即使调整以前赋值的其他变量都没用），所以这个算法是没有回溯过程的。

struct TwoSat {
    static const int MAX_NODE = 1000;
    vector<int> G[MAX_NODE];
    int n, stk[MAX_NODE], sz;
    bool mark[MAX_NODE];

    void init(int _n) {
        n = _n;
        for (int i = 0; i < n * 2; ++i) G[i].clear();
        memset(mark, 0, sizeof(mark));
    }

    void addClause(int x, int xVal, int y, int yVal) {
        x = x * 2 + xVal, y = y * 2 + yVal;
        G[x ^ 1].push_back(y);
        G[y ^ 1].push_back(x);
    }

    bool dfs(int x) {
        if (mark[x ^ 1]) return false;
        if (mark[x]) return true;
        stk[sz++] = x;
        mark[x] = true;
        for (int i = 0; i < (int)G[x].size(); ++i)
            if (!dfs(G[x][i])) return false;
        return true;
    }

    bool solve() {
        for (int i = 0; i < n * 2; i += 2)
            if (!mark[i] && !mark[i ^ 1]) {
                sz = 0;
                if (!dfs(i)) {
                    while (sz > 0) mark[stk[--sz]] = false;
                    if (!dfs(i ^ 1)) return false;
                }
            }

        return true;
    }
};

扩展

2-SAT 问题添加的条件只能是 ‘或’ ，即两个之中有一个成立即可，但我们可以通过添加多条‘或’语句，来表示其他逻辑关系。

与二分图染色的区别

其实一开始学习 2-SAT 的时候，我成功的把 2-SAT 与二分图染色搞混了，然后琢磨着用并查集写，结果不幸的错了。现在说一说它们的区别。
二分图染色表示的是变量之间不能共存的关系，假定染色成黑色是值 $true$，染成白色就是值为 $false$。如果 $a,b$ 不能共存，那么就在 $a, b$ 之间连一条无向边，使得它们的颜色不能相同，自然值不相同。在这个问题中若 $a$ 是白，一定可以推出 $b$ 是黑。若 $b$ 是黑，一定可以推出 $a$ 是白。
接着观察 2-SAT 问题的条件，$x == xval\,||\,y == yval$，如果 ，我们一定可以推出 $y == yval$，这个推导是有向的，我们不能从 $y == yval$ 中推出 。所以 2-SAT 的条件在二分图染色中无法实现。另外一个致命的原因则是二分图染色是一旦有矛盾立即跳出，而 2－SAT 则是有矛盾之后更换取值继续操作。
如果把二分图染色中的边换成有向边可不可以呢，仔细想一想，这是没有意义的。
但有一种情况，是可以用二分图染色处理的，当且仅当所有条件是 $x == k\,||\,y == k$ 的形式，即变量的值一样。这个条件也可以写成 $(x == !k\, \&\& \,y == !k) == false$。嗯？这不就是说的 $x,y$ 不能同时等于 $!k$ 吗？相当于 $x,y$ 不能共存（$k == false$ 时是不能共存，$k == true$ 时是不能同时不存在，这两种也是可以相互转化的），于是问题成功的转化成了二分图染色的模型，也就可以放心的使用二分图染色求解了（happy！！！

例题

由于 2-SAT 问题的模式相对固定，辨识度也比较高，所以这样的题目并不是很多，单独也不大。下面的几个例题基本囊括了大部分题目了，难度也是循序渐进的，强烈建议全部搞懂。

POJ 3678 - Katu Puzzle

题目地址
有 $n (n\le1000)$ 个变量，给出一些条件 （‘AND’，‘OR’，‘XOR’）以及值，问能否对这些变量赋值，使得条件全部满足。满足输出 YES，否则输出 NO。

分析

用刚刚说的扩展里面的内容就行了，对每条语句进行讨论即可，一共六种情况，比较基础的条件组合。

POJ 3207 - Ikki's Story IV - Panda's Trick

题目地址
平面上，一个圆，圆的边上按顺时针放着 $n(n\le1000)$ 个点。现在要连 $m(m\le500)$ 条边，比如 $a$，$b$，那么 $a$ 到 $b$ 可以从圆的内部连接，也可以从圆的外部连接。给你的信息中，每个点最多只会连接一条边。问能不能找到连接这 $m$ 条边的方式（圆外连或者圆内连） ，使这些边都不相交。

分析

题意要明白，看图就懂了：

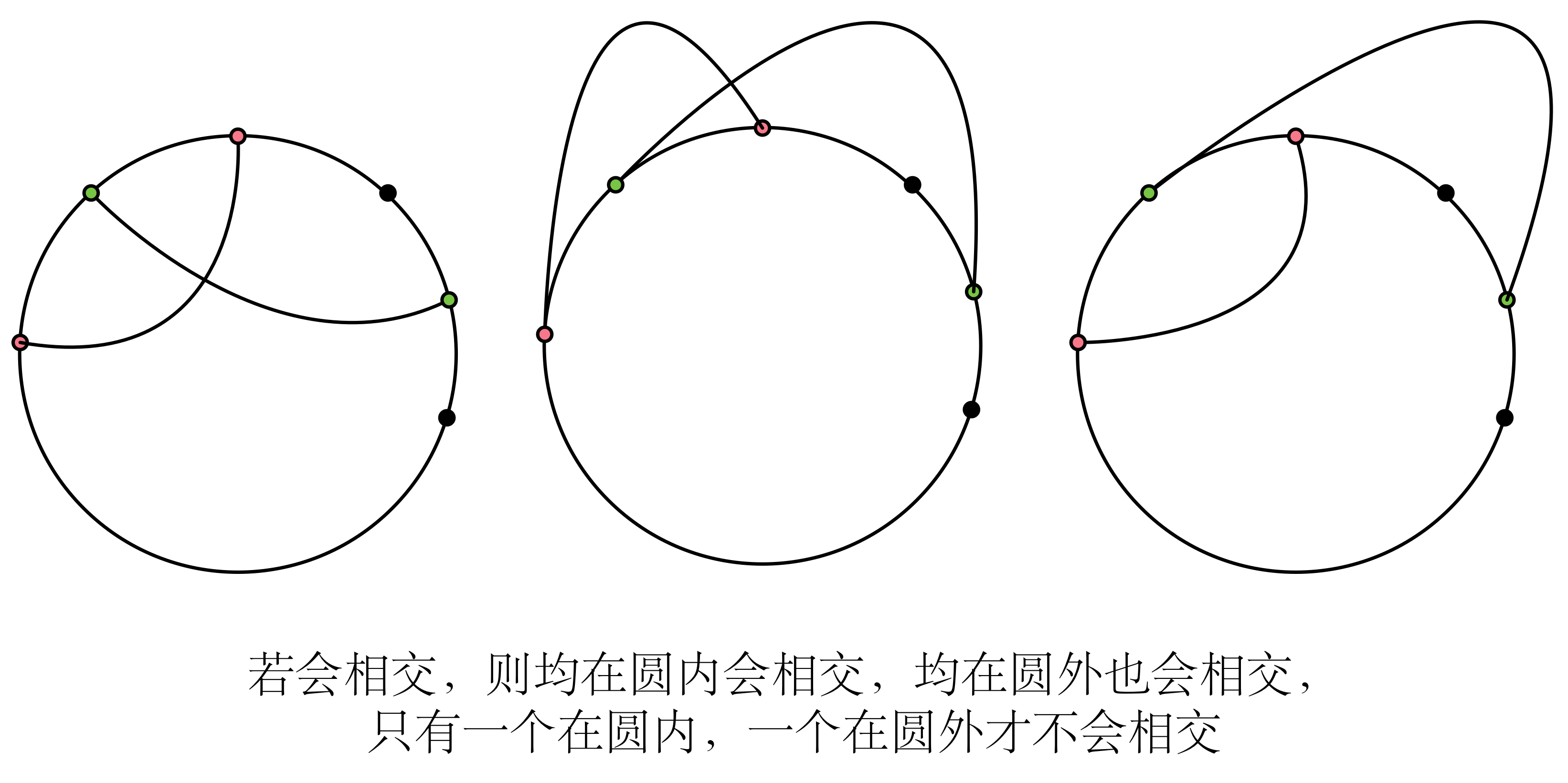
判断线段 $(a, b), (c, d)$ 相交的条件是 $(a-c)(b-c)(a-d)(b-d) < 0$ ，请注意溢出！
于是转化为了经典的不共存问题（2-SAT的特殊情况），可用二分染色或并查集解决，用 2-SAT 的解法也可。

POJ 2723 - Get Luffy Out

题目地址
有 $m(m\le2048)$ 层楼，从一层到 $m$ 层，要进入每层都要打开位于该层的两道门中的至少一道。门锁有 $2n(n\le1024)$ 种，每个门锁为 $2n$ 种中的一种，可以重复。有 $2n$ 把钥匙，分别对应 $2n$ 种锁，但是钥匙两两一组，共 $n$ 组，每组只能选一个来开门，被选中的可以多次使用，另一个一次都不能用。问最多能上多少层？

分析

二分能上到的楼层 $T$，然后建图，每把钥匙为一个点，首先添加条件使得同一串的两把钥匙不能同时用($x == false\,||\,y == false$)。然后是门，每扇门拆为两个节点，对应两把锁，两把锁之间必有一把被开（值为 $true$）($x == true\,||\,y == true$)。然后是开锁，如果 $a$ 能开 $b$，则 $a$ 与 $b$ 一定是相等的，扩展中提到了让变量相等的做法。最后判断是否矛盾即可，思考量有一些。
不过根据题目的特殊性，$2n$ 把钥匙一一对应 $2n$ 种锁，可以只设置 $2n$ 个节点来表示锁。每把锁有两个状态（开或没开) 。一样的限制条件，同一串的两把钥匙不能同时用（对应的锁不能同时被开）和每扇门对应两把锁之间必有一把被开。

POJ 3683 - Priest John's Busiest Day

题目地址
一个小镇里面只有一个牧师，现在有些新人要结婚，需要牧师分别去主持一个仪式，给出每对新人婚礼的开始时间 $s$ 和结束时间 $t$ ，还有他们俩的这个仪式需要的时间（每对新人需要的时间长短可能不同）$d$ ，牧师可以在婚礼开始的时间 $d$ 内（$s$ 到 $s+d$）或者是结束前的时间 $d$ 内（$t - d$ 到 $t$）完成这个仪式。现在问能否给出一种安排，让牧师能完成所有夫妇婚礼的仪式，如果可以，输出一种安排。

分析

每场婚礼为一个变量，$false$ 表示开始时举行仪式， $true$ 表示结束时举行仪式，对于有矛盾的时间，添加条件使其不能同时被选中即可（想一想这为什么不是不共存问题）。

UVa 1146 - Now or later

题目地址
$n(n\le2000)$ 班飞机，每个飞机有一个早到时间和一个晚到时间，问怎么安排飞机，使得飞机到的间隔的最小值最大？

分析

二分时间间隔 $t$。每班飞机为一个变量，$false$ 表示早到，$true$ 表示晚到。枚举每两个飞机之间的情况（4种），有冲突则添加条件使其不能一起选择。最后判断是否矛盾即可。

POJ 2749 - Building roads

题目地址
给出 $n(n\le500)$ 个牛棚的坐标，两个中转点 $S1, S2$ 的坐标。$S1, S2$ 之间联通。现在要使牛棚之间联通，但每个牛棚只能连接 $S1$ 或 $S2$。除此之外，某些牛是好朋友，其牛棚只能连在同一个中转点。某些牛相互憎恨，这些牛棚不能连在同一个中转点。要使条件满足的情况下，最长的牛棚间距离最小，并输出这个距离。（题中距离均是曼哈顿距离 $|x1 - x2| + |y1 - y2|$）

分析

还是二分答案 $d$。每个牛棚为一个变量，$false$ 表示连接 $S1$， $true$ 表示连接 $S2$。对于有冲突的牛，不能连同一个中转点，值不能相等。对于是好朋友的牛，必须连同一个中转点，值必须相等。枚举两头牛之间的选择（4种情况），如果不行，就添加条件使其不能同时选择。最后判断是否矛盾就行了。

1391 - Astronauts

题目地址
有 $n(n\le100000)$ 个宇航员，按照年龄划分，年龄低于平均年龄的是年轻宇航员，而年龄大于等于平均年龄的是老练的宇航员。现在要分配他们去A，B，C三个空间站，其中A站只有老练的宇航员才能去，而B站是只有年轻的才能去，C站都可以去。有 $m(m\le100000)$ 对宇航员之间相互讨厌，不能让他们在同一个空间站工作。输出每个宇航员应分配到哪个空间站，如果没有可行的方案则输出 No solution.。

分析

这题的建图有些不一样了，对于 $true, false$ 每个点的含义不同，不过可以解决。每个宇航员只有两种选择，所以每个宇航员为一个变量，老练的宇航员 $false$ 表示做C，$true$ 表示做A。年轻的宇航员 $false$ 表示做C，$true$ 表示做B。
对于互相讨厌的宇航员，若属于同一类型，则它们做的任务必须不同。若不属于同一类型，则它们至少有一个为 $true$ 即可（唯一冲突的是都做C)。

POJ 3648 - Wedding

题目地址
有一对新人结婚，邀请 $n(n\le30)$ 对夫妇去参加婚礼。有一张很长的桌子，人只能坐在桌子的两边，还要满足下面的要求：首先，每对夫妇不能坐在同一侧。然后，$n$ 对夫妇之中可能有通奸关系（包括男男，男女，女女），有通奸关系的不能同时坐在新娘的对面，可以分开坐，可以同时坐在新娘这一侧。如果存在一种可行的方案，输出与新娘同侧的人。

分析

每对夫妇为一个变量，$false$ 表示妻子和新娘坐在同侧（意味着丈夫与新郎坐在同侧），$true$ 则表示妻子和新郎坐在同侧（意味着丈夫与新娘坐在同侧）。然后一开始应该让 $mark[0] = true$，固定新娘的位置。做了上面的好几个题，通奸关系应该很好添加条件了，请自己思考（其实是懒得写了。。

总结

题目中，2-SAT 问题一般会以这样的情景出现：只有两种选择、有一些限制关系、最大化最小值、最小化最大值。所以，正确的识别 2-SAT 问题以及按照具体情境构图是关键，构好图，问题自然迎刃而解。