网络流之 - 消圈定理（POJ 2175）

Published on 2015-12-05

摸爬滚打研究了好几个小时，终于搞清楚了消圈定理，其实并不复杂。。

消圈定理

所谓消圈定理，就是在某个流 $f$ 中，如果其对应的残余网络没有负圈（剩余流量为 $0$ 的边视为不存在），那它一定就是当前流量下的最小费用流。反之亦然。即「 $f$ 是最小费用流等价于其残余网络中没有负圈」。

证明

怎么证明？

假设任意流 $f$ ，如果在相同流量下有比他更小费用的流 $f'$ 。观察流 $f' - f$ ，在流 $f$ 中，除源汇外所有点的流入量等于流出量，在流 $f'$ 中亦然，即流 $f' - f$ 是由若干圈构成的。因为流 $f' - f$ 的费用是负的，所以在流 $f' - f$ 中，必定至少有一个负圈。

摘自日本人的书，可能有点不好理解。让我们用更直观的方式考虑。

假设一个网络是这样的，为方便起见，所有边的容量都是 $1$ 。

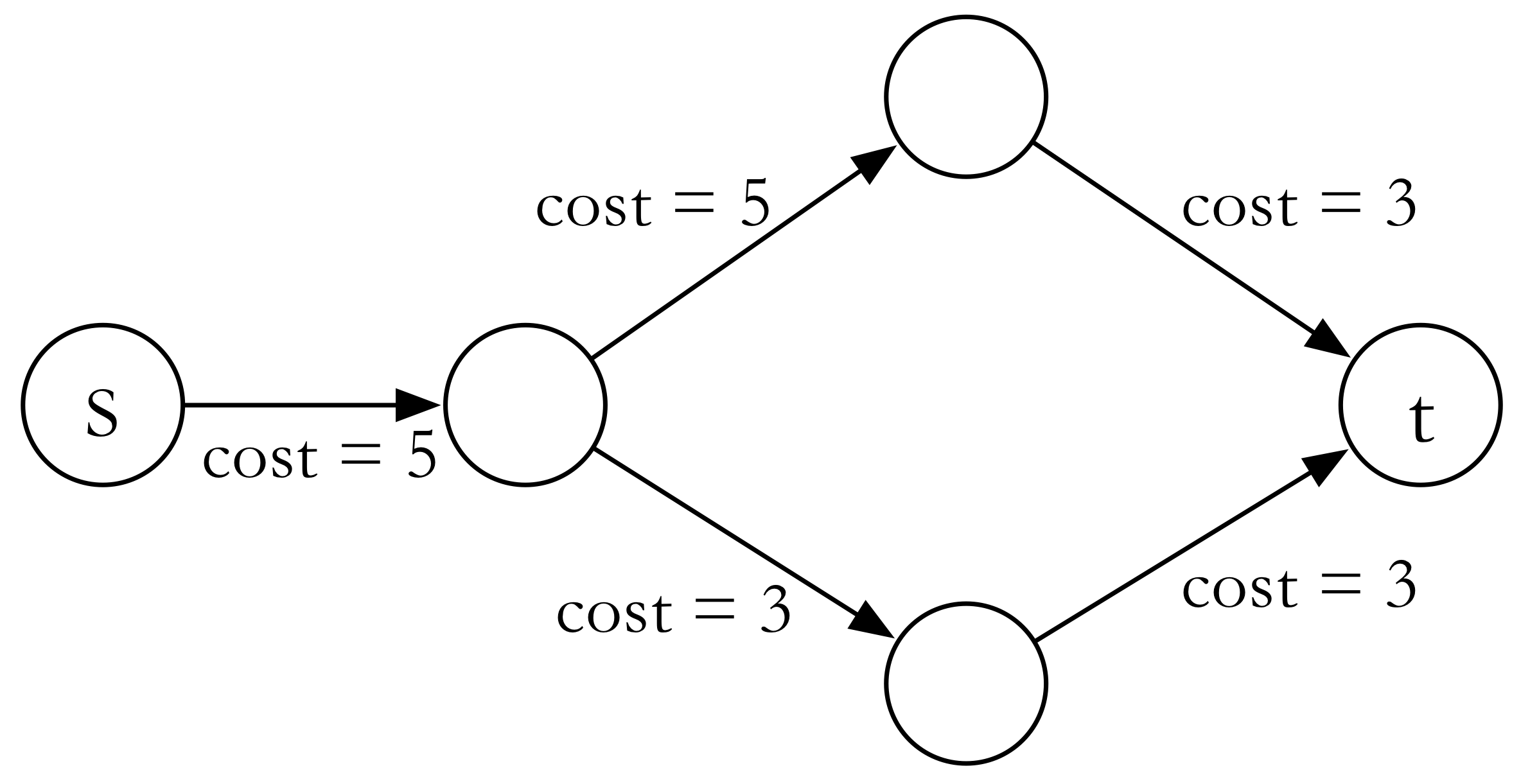
如果流量走上路的话，其残余网络（没有特别说明的话，考虑的都是残余网络）看起来应该是这样的：

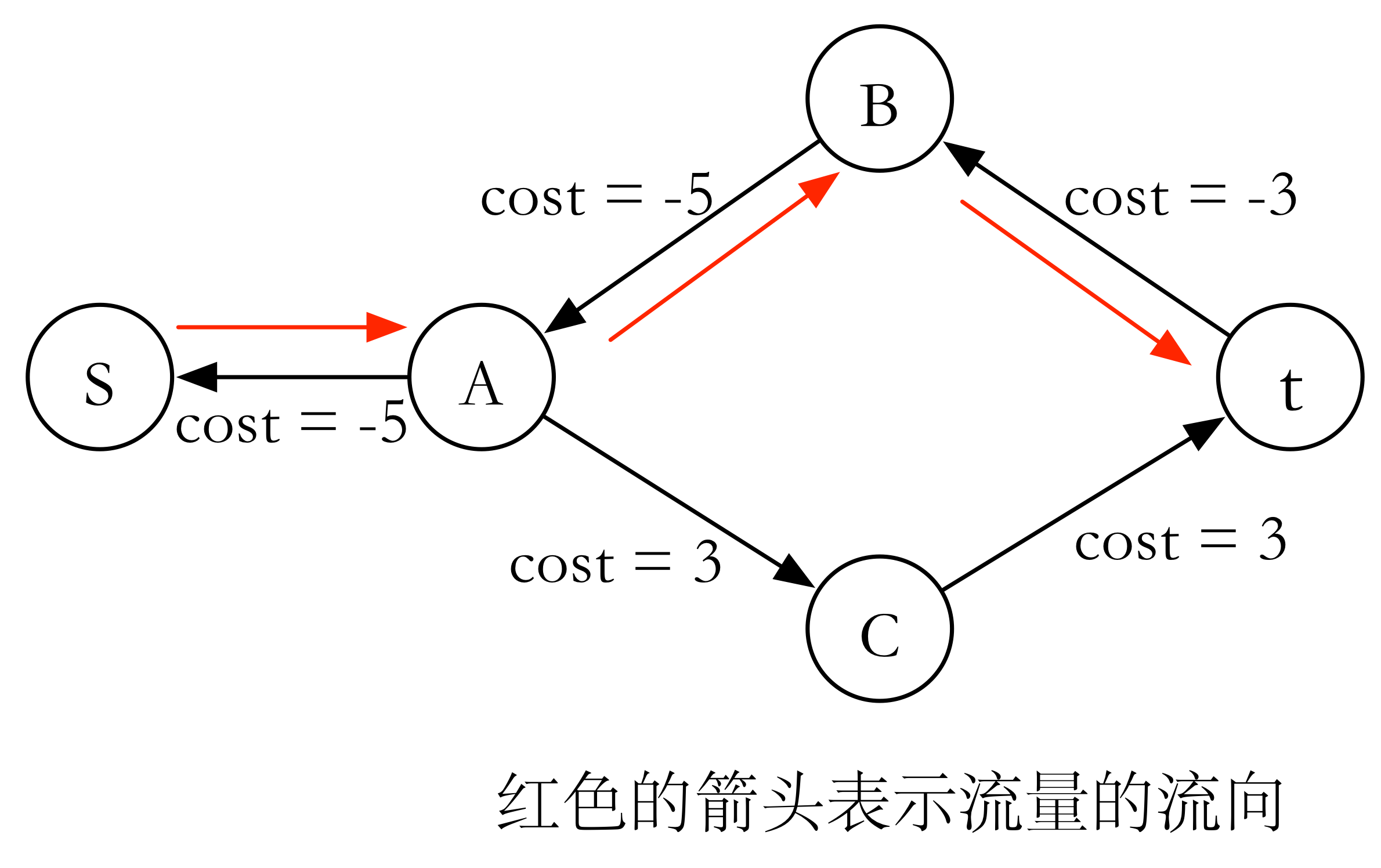
因为上路的边的流量占满了，所以现在上路只有反边。明显看到 $A \rightarrow C \rightarrow t \rightarrow B \rightarrow A$ 是一个大大的负圈。我们沿着此负圈增广（每条边的流量＋1），可以得到当前流量下的最小费用流。
正确性很好证明。原流中，除了源点以及汇点每个点的入流量等于出流量，这个流一定是可行流。沿着负圈增广之后，除了源点以及汇点每个点的入流量仍然等于出流量。
就拿顶点 $A$ 来说，原图中 $A$ 的出入流量均为 $1$ ，增广之后，有 $1$ 的流量从 $A$ 流入 $C$ ，但是，却有 $1$ 的流量从 $B$ 流回 $A$ 。
一番下来， $A$ 的出入流量仍然相等，还是 $1$ 。不难证明其它顶点均如此，所以消圈后既保证了这个流是可行流，又减少了费用，所以它是正确的。
为了加深理解，对应下图，流量在圈中增广，总的流量既没有增加，也没有减少，只不过是流量从费用更少的地方流过（ $A \rightarrow C \rightarrow t$ ），从费用大的地方退流而已（ $t \rightarrow B \rightarrow A$ ），流过的流量和退掉的流量是相等的。实质上是将从 $A$ 流出的流量的方向改变，使得费用更小。
网络流的反边给了我们一个很好的反悔机制，使得我们可以对任意一个流 $f$ ，通过消负圈（可能不止一个），来得到它当前流量下的最小费用流。

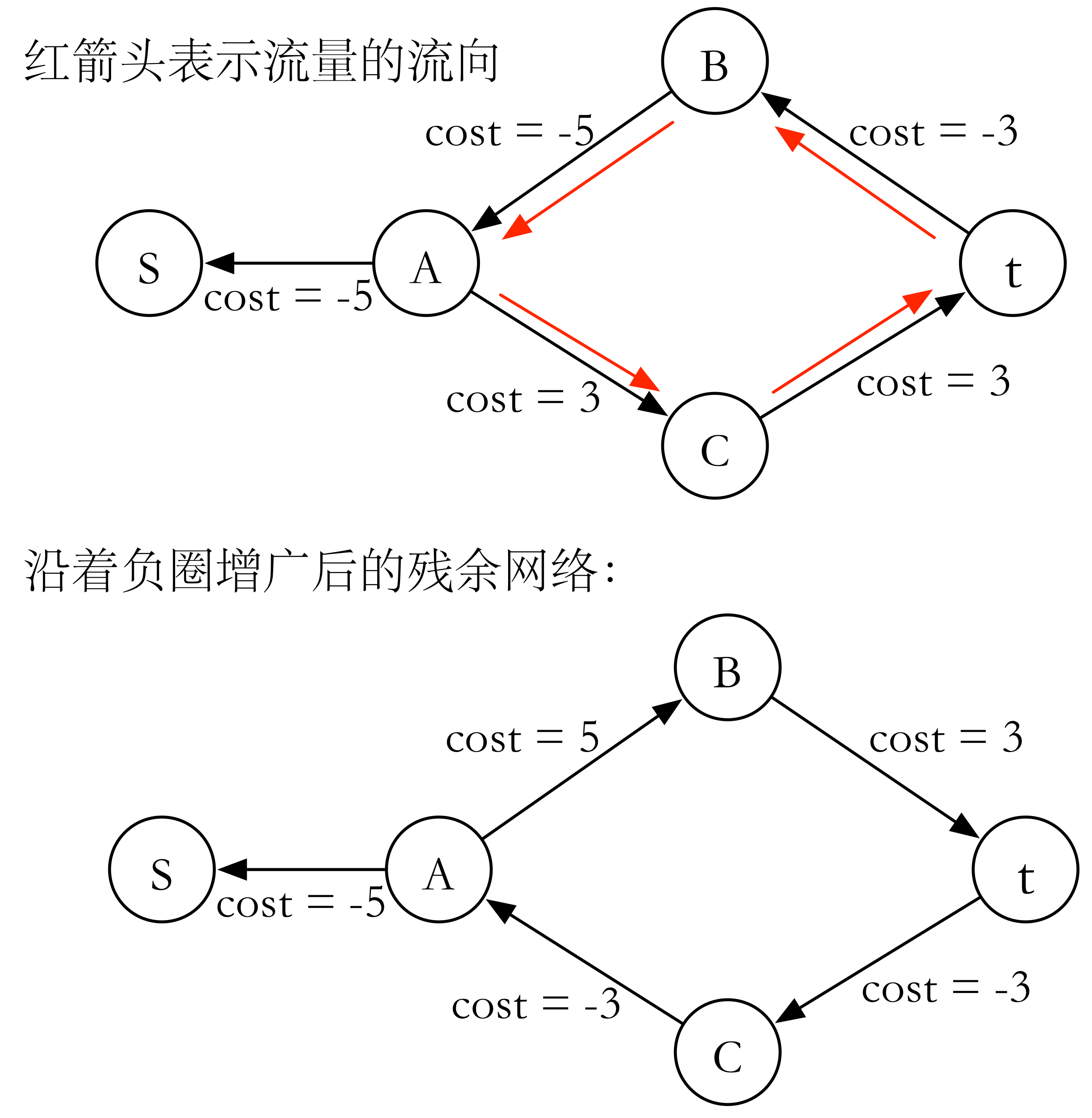
可以看到，沿着负圈增广之后，已经没有负圈存在了，已经达到了当前流量下的最小费用流（也就是最小费用最大流）。所以只要有负圈，就可以增广达到更小费用。反之亦然，所以有「 $f$ 是最小费用流等价于其残余网络中没有负圈」

应用

前面说了对任意一个流 $f$ ，可以通过消负圈，来得到它当前流量下的最小费用流。问题来了，怎么找负圈？残余网络可能不是联通的，因此从谁出发都不确定。既然不确定，我们添加一个超级源点 $Su$ ，给每一个顶点 $v$ 连一条从 $Su \rightarrow v$ 的有向边，权值为 $0$ ，容量无限大（想一想为什么不能是无向边），从 $Su$ 出发，令 $dis(Su) = 0$ 。这样就保证了图的联通性。
再将 $Bellman-Ford$ 算法执行 $n$ 次， $n$ 为顶点数（含 $Su$ ）。同时记录每个顶点的前驱节点 $prevv[v]$ ，以及对应的边 $preve[v]$ 。如果第 $n$ 次仍然有顶点被更新，那么残余网络中一定有负圈。
如果没有负圈，最坏的情况是链式结构，每次只更新一个顶点，共需要 $n - 1$ 次，所以如果第 $n$ 次仍然被更新，那说明被更新的顶点 $v$ 的前驱中一定有负圈（它不一定在负圈上），那我们只需要不断的找它的前驱节点，每经过一个节点标记一次，那么一旦一个节点 $A$ 被经过 $2$ 次，节点 $A$ 一定在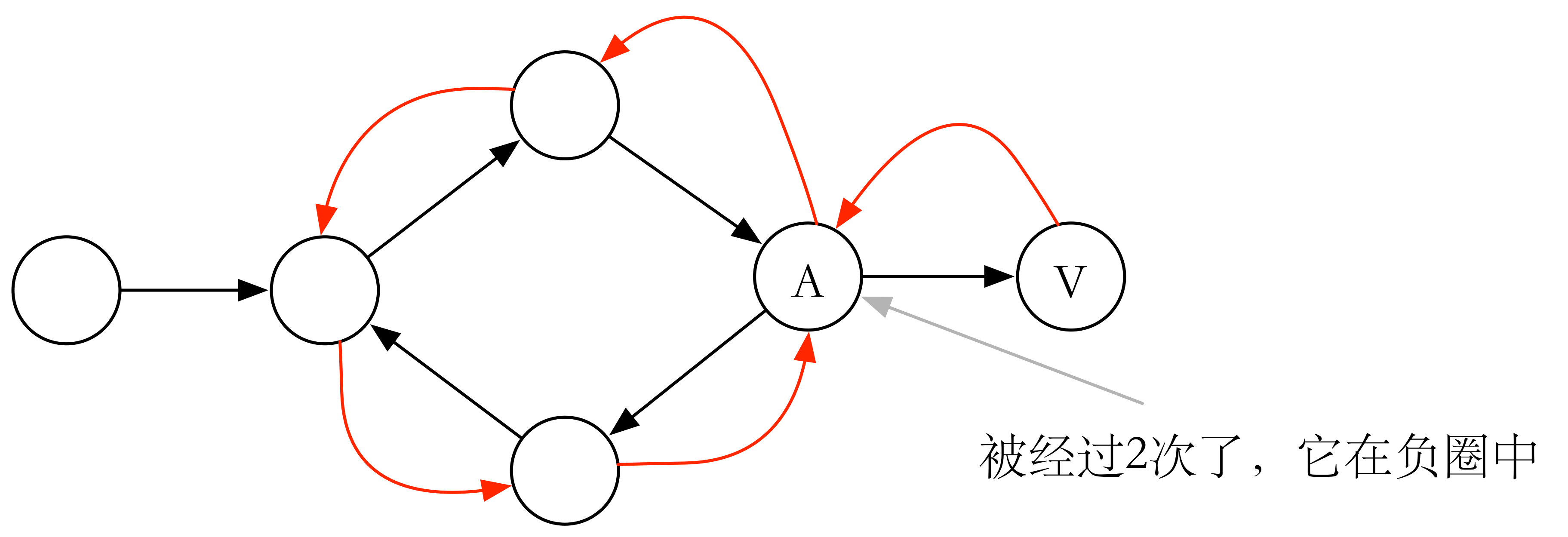负圈中。

但用不着这么麻烦，既然超级源点到每个顶点的边权都是 $0$ ，我们不妨直接让所有顶点的 $dis$ 直接为 $0$ ，这样是等效的，而且避免的加边带来的麻烦。具体操作就是让所有的 $dis = 0$ ，顶点数量 $n$ 还是原来的顶点数（ $Su$ 已经不存在了），然后跟之前一样用 $Bellman-Ford$ 就行了。
当然 $SPFA$ 也可以，不过条件要改成顶点入队的次数为 $n$ 。

遍历负圈也是一样的方法，从刚刚找到的在负圈的节点 $A$ 开始，通过 $G[prevv[cur]][preve[cur]]$ 找到这条边让其流量 +1（别忘了修改反边），再走到前驱节点，如果当前节点又是 $A$ 则跳出。具体细节见代码。

POJ 2175 Evacuation Plan

原题地址
有了消圈定理，这个题就好办了。题目以及构图大家自己想。根据题目给的方案直接构造出残余网络（加边的时候直接传入当前流量即可），然后找一个负圈增广，如果没找到说明已经最优，否则增广以后输出方案即可。

代码

//  Created by Sengxian on 12/4/15.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
//  Poj 2175 最小费用流 + 消圈定理
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#include <cmath>
using namespace std;
const int INF = 0x3f3f3f3f, maxn = 105, maxm = 105;

inline int ReadInt() {
    int n = 0, ch = getchar(); bool flag = false;
    while(ch < '0' || ch > '9') {
        if(ch == '-') flag = true;
        ch = getchar();
    }
    do {
        n = n * 10 + ch - '0';
        ch = getchar();
    }while(ch >= '0' && ch <= '9');
    if(flag) return -n;
    return n;
}

int N, M, bx[maxn], by[maxn], b[maxn], hx[maxm], hy[maxm], c[maxm], e[maxn][maxm];
int OriCost = 0, tot = 0;

inline int Cost(int i, int j) {
    return abs(bx[i] - hx[j]) + abs(by[i] - hy[j]) + 1;
}

struct edge {int to, cap, cost, rev;};
struct MCMF {
    static const int maxNode = maxn + maxm + 2;
    vector<edge> G[maxNode];
    int dis[maxNode], prevv[maxNode], preve[maxNode], n;
    bool inq[maxNode], vis[maxNode];
    void add(int f, int t, int cap, int cost, int used) {
        G[f].push_back((edge){t, cap - used, cost, G[t].size()});
        G[t].push_back((edge){f, used, -cost, G[f].size() - 1});
    }
    bool clearCircle() {
        memset(dis, 0, sizeof(dis));
        memset(vis, 0, sizeof(vis));
        int in = -1;
        for(int t = 0; t <= n; ++t)
            for(int cur = n - 1; cur >= 0 && in == -1; --cur)
                for(int i = 0; i < G[cur].size(); ++i) {
                    edge &e = G[cur][i];
                    if(e.cap > 0 && dis[e.to] > dis[cur] + e.cost) {
                        dis[e.to] = dis[cur] + e.cost;
                        prevv[e.to] = cur;
                        preve[e.to] = i;
                        if(t == n) {
                            in = cur;    
                            break;
                        }
                    }
                }
        if(in == -1) return false; //没有找到负圈
        while(!vis[in]) {
            if(vis[in] == true) break;
            vis[in] = true;
            in = prevv[in];
        }
        //开始消圈
        int cur = in;
        do {
            edge &e = G[prevv[cur]][preve[cur]];
            e.cap--;
            G[e.to][e.rev].cap++;
            cur = prevv[cur];
        }while(cur != in);
        return true;
    }
}MCMF;

void Solve() {
    int s = N + M, t = N + M + 1;
    for(int i = 0; i < N; ++i)
        for(int j = 0; j < M; ++j)
            MCMF.add(i, j + N, INF, Cost(i, j), e[i][j]);
    for(int i = 0; i < N; ++i)
        MCMF.add(s, i, b[i], 0, b[i]);
    for(int j = 0; j < M; ++j) {
        int sum = 0;
        for(int i = 0; i < N; ++i) sum += e[i][j];
        MCMF.add(j + N, t, c[j], 0, sum);
    }
    MCMF.n = M + N + 2;
    if(MCMF.clearCircle()) {
        printf("SUBOPTIMAL\n");
        for(int i = 0; i < N; ++i)
            for(int j = 0; j < M; ++j) {
                edge &e = MCMF.G[i][j];
                printf("%d%c", MCMF.G[e.to][e.rev].cap, j + 1 == M ? '\n' : ' ');
            }
    }else printf("OPTIMAL\n");
}


int main() {
    N = ReadInt(), M = ReadInt();
    for(int i = 0; i < N; ++i)
        bx[i] = ReadInt(), by[i] = ReadInt(), tot += (b[i] = ReadInt());
    for(int i = 0; i < M; ++i)
        hx[i] = ReadInt(), hy[i] = ReadInt(), c[i] = ReadInt();
    for(int i = 0; i < N; ++i)
        for(int j = 0; j < M; ++j)
            OriCost += Cost(i, j) * (e[i][j] = ReadInt());
    Solve();
    return 0;
}

2-SAT 问题绝对众数问题

Sengxian's Blog