Sengxian's Blog

绝对众数。在数列 $p$ 中出现次数严格大于 $\frac{\vert p \vert}{2}$ 的数叫做绝对众数。

求绝对众数

快速排序

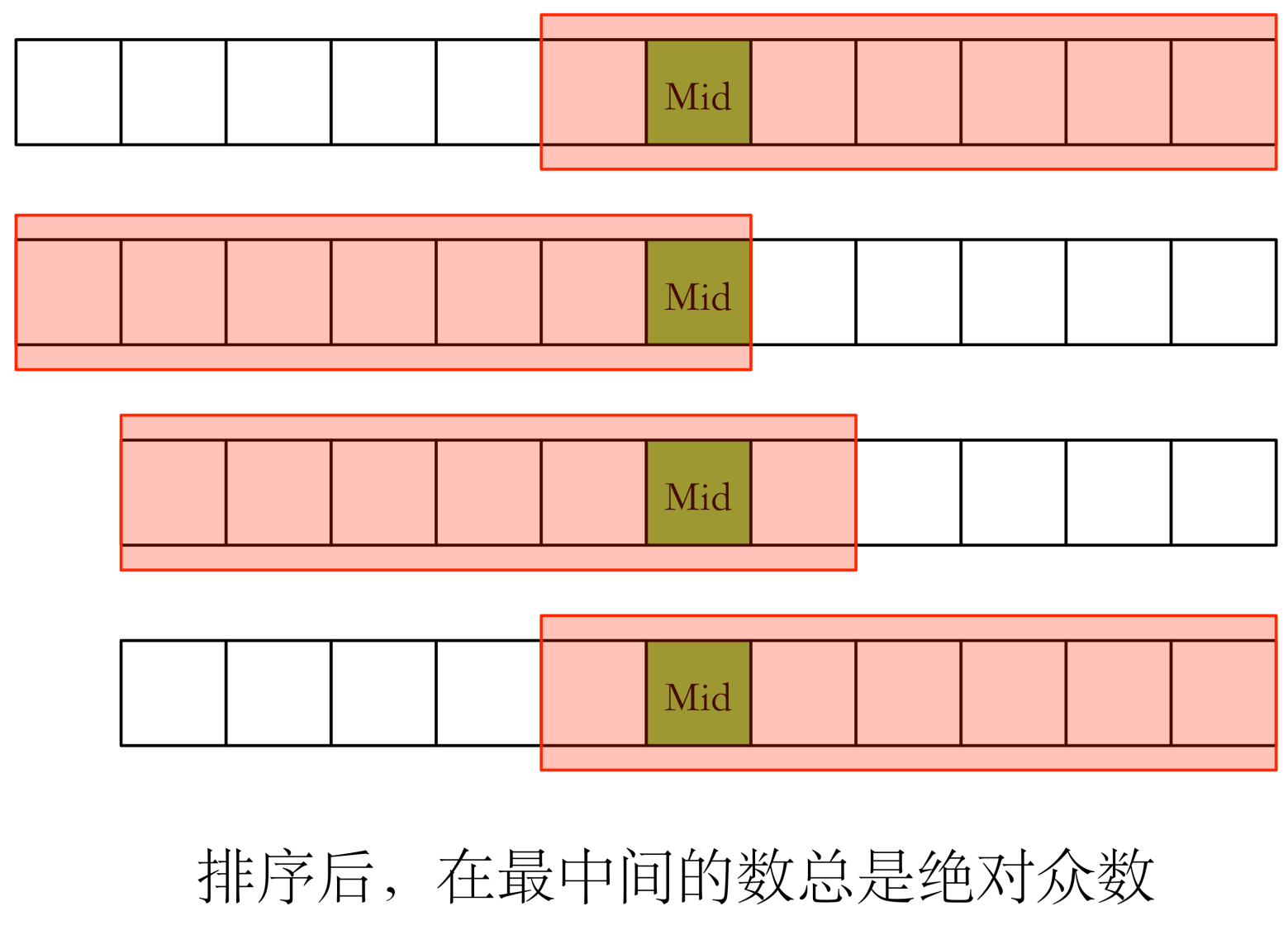
对数列 $p$ 快速排序，如果存在绝对众数的话，最中间的数一定是绝对众数。
复杂度 $O(n\log n)$。

摩尔投票法

摩尔投票法的基本思想很容易理解，在每一轮投票过程中，从数组中找出一对不同的元素，将其从数组中删除。循环执行这一操作，直到无法再进行投票，如果数组为空，则没有任何元素出现的次数超过该数组长度的一半（无绝对众数）。如果只存在一种元素，那么这个元素则可能为绝对众数。
在编写算法的过程中，我们可以直接按照数组原来的顺序进行投票，删除。
具体实现：设 $num$ 为当前出现阶段超过半数的元素（候选数），$cnt$ 为此元素出现次数。由于有了阶段的概念，这其实这也是一种动态规划思想。
一开始 $num$ 直接为数组第一个元素，$cnt = 1$。（原因是只有一个元素的数组，唯一的那个元素一定是绝对众数）
接着遍历数列 $p$，设当前数为 $k$。

• 若 $k = num$，则 $cnt + 1$。
• 若 ，则我们可以把当前候选数和当前数同时删除，具体操作就是让 $cnt - 1$，这样就相当于忽略了数 $k$，删去一个 $num$。
• 若 $cnt = 0$，表明前一阶段并没有出现次数超过半数的元素。假设绝对众数存在，那么绝对众数一定在剩余的数组中是绝对众数，这样我们只需要求解原始问题的子问题即可，即在后一阶段的绝对众数是多少。回到开始， $num$ 为当前元素，$cnt = 1$。

最终，若 $cnt > 0$，则 $num$ 可能为候选元素。扫一遍数组确认一下即可。
复杂度为线性的，$O(n)$。

代码

void majorityElement(vector<int>& p) {  
    int num = -1, cnt = 0;
    for(int i = 0; i < p.size(); ++i) {
        if(cnt == 0) num = p[i], cnt++;
        else if(p[i] == num) cnt++;
        else cnt--;        
    }
    cnt = 0;
    for(int i = 0; i < p.size(); ++i)
        if(p[i] == num) cnt++;
    if(cnt > p.size() / 2) printf("Found: %d\n", num);
    else printf("Not Found\n");
}