二分搜索

Published on 2015-10-18

二分搜索法，是通过不断缩小解可能存在的范围，从而求得问题最优解的方法。其应用非常广泛，不仅可以迅速在有序数列中查找一个值，更可以进行其他的操作。下面说一说二分。

从有序数组中查找某个值

lower_bound & upper_bound

函数 lower_bound() 在给定单调不下降序列，位置 first 和 last 形成的前闭后开区间进行二分查找，返回大于或等于val的第一个元素位置。如果所有元素都小于val，则返回last的位置
输入: a = {2, 3, 3, 5, 6} target = 3
输出: 1

当然，如果朴素地按照顺序逐个查找的话，当然可以求得答案。但如果利用序列的有序性这一条件，就可以获得更为高效的算法。
首先我们看第 $\frac{n}{2}$ 个数，如果它大于等于 $target$ ，那么可以知道解不大于 $\frac{n}{2}$ ，反之，我们可以知道解一定大于 $\frac{n}{2}$ 。每次与中点比较可以把解的范围缩小一半，最终可以在 $O(\log_2n)$ 次的比较之内求的最终的解。

int lowerbound(int nums[], int start, int end, int target) {
    int lb = start - 1, ub = end;
    while(ub - lb > 1) {
        int mid = (lb + ub) / 2;
        if(nums[mid] >= target)
            ub = mid; //如果中间的数要大于等于目标数，那么解的范围变为 (lb, mid]
        else lb = mid; //否则，解的范围变为 (mid, ub]
    }
    // 此时 ub = lb + 1
    // 由前可知，解的范围为(lb, ub]，答案就是 ub
    return ub;
}

这种算法被称为二分搜索。此外，STL 中以函数 lower_bound 实现了二分搜索。
同样，也有一个函数叫 upper_bound，它返回大于或等于 $val$ 的第一个元素位置，实现起来与上面的代码几乎没有区别，不过是把 if 语句中改为大于号而已。

int upperbound(int nums[], int start, int end, int target) {
    int lb = start - 1, ub = end;
    while(ub - lb > 1) {
        int mid = (lb + ub) / 2;
        if(nums[mid] > target)
            ub = mid; //如果中间的数要大于目标数，那么解的范围变为 (lb, mid]
        else lb = mid; //否则，解的范围变为 (mid, ub]
    }
    // 此时 ub = lb + 1
    // 由前可知，解的范围为(lb, ub]，答案就是 ub
    return ub;
}

我们来测试一下

int main() {
    cout << lowerbound(a, 0, 5, 3) << endl;
    cout << upperbound(a, 0, 5, 3) << endl;
    return 0;
}

结果分别是1和3。这里有个小技巧，要求单调序列中数 k 的个数，一句话就可以搞定（这里使用STL中的二分搜索）

upper_bound(a, a + n, k) - lower_bound(a, a + n, k)

所以二分搜索不仅快捷，而且方便。

二分搜索的更多应用

二分除了在有序数列中查找值之外，对于求解最优解的题目也很有用。如果对于任意满足 $C(x)$ 的x，如果所有的 $x^{'} > x$ 都有 $C(x^{'})$ 成立，那么我们就可以根据二分搜索求出最优解。

最小化最大值

根据之前所分析的，如果对于任意满足 $C(x)$ 的 $x$ ，如果所有的 $x^{'} > x$ 都有 $C(x)$ 成立。这种问题叫做最小化最大值问题。其实很好理解， $C(x)$ 表示 $x$ 是否可以成立，当值逼近无穷大时，它肯定可以成立，我们要寻找的是最小的 $x$ ，使 $C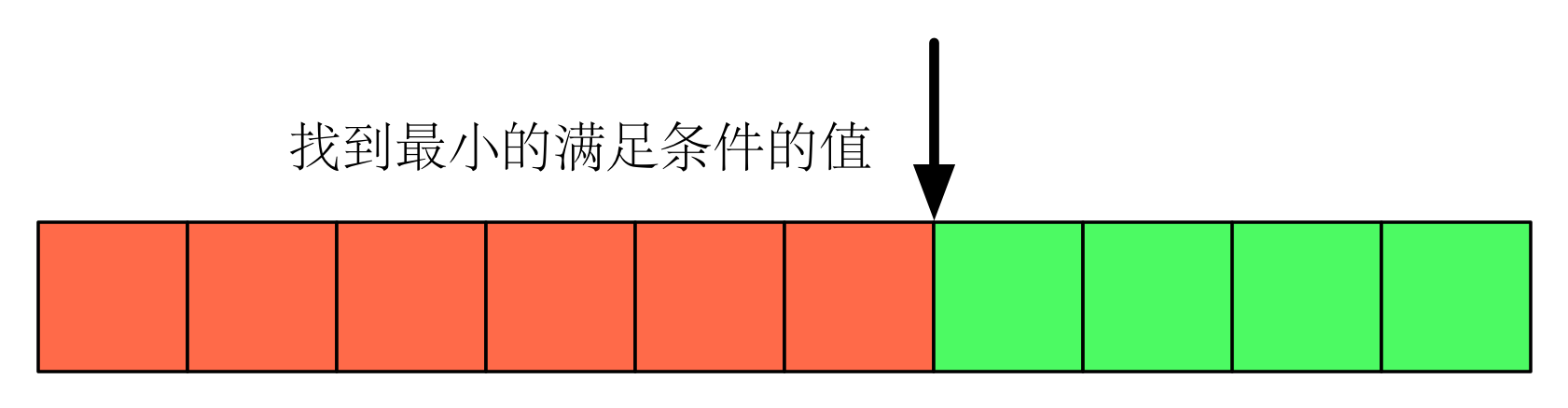(x)$ 成立。

Aggressive cows(Poj No.2456)

农夫约翰搭了一间有N间牛舍的小屋。牛舍被排在一条线上，第i 号牛舍在xi的位置。但是他的M头牛对小屋很不满意，因此经产互相攻击。约翰为了防止牛之间互相伤害，因此决定把每头牛都放在离其他牛尽量远的牛舍。也就是要最大化最近的两头牛之间的距离。

分析

使 $C(d)$ 可以安排你牛的位置使得最近的两头牛的距离不小于 $d$
问题就变为求满足 $C(d)$ 最大的 $d$ ，用刚刚的模型即可。由贪心可以知道在满足条件的情况下，两头牛尽量靠近，运用贪心可以判断 $C(d)$ 是否成立。
代码清晰易懂，想一想，为什么输出 $lb$ ？

//  Created by Sengxian on 15/10/18.
//  Copyright (c) 2015年 Sengxian. All rights reserved.
#include <algorithm>
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 100000 + 5;
int c, n;
int pos[maxn];

bool C(int a) {
    int lastcow = 0; //上一头牛所在位置 
    for(int i = 1; i < c; ++i) {
        int nowcow = lastcow + 1;
        while(nowcow < n && (pos[nowcow] - pos[lastcow]) < a)
            nowcow++;
        if(nowcow == n) return false;
        lastcow = nowcow;
    }
    return true;
}

int main() {
    int lb = 0, ub = 0;
    scanf("%d%d", &n, &c);
    for(int i = 0; i < n; ++i) {
        scanf("%d", &pos[i]);
        ub = max(ub, pos[i]);    
    }
    sort(pos, pos + n);
    while(ub - lb > 1) {
        int mid = (lb + ub) / 2;
        if(C(mid)) lb = mid; //如果mid距离合适，解的范围变成 [mid, ub)
        else ub = mid; //如果不合适，解的范围变成 [lb, mid)
    } 
    printf("%d\n", lb); //左边的一定可以！
    return 0;
}

弹性碰撞