弹性碰撞
Published on 2015-10-25最近做了一些弹性碰撞的题目,然而大多数的书或者博文都没有详细的分析,做的迷迷糊糊的。费尽心思搞懂之后,决定分享一下心得,其实并没有多难。
定义
弹性碰撞是指两个刚体(忽略大小)在同一直线上运动时,相撞没有能量损耗,交换各自的速度同时掉头运动。
基本思想
处理这种问题,首先要明白基本的两点:
- 引理一:忽略个体的差异,那么两个刚体相撞掉头可以看作保持原样运动擦身而过。
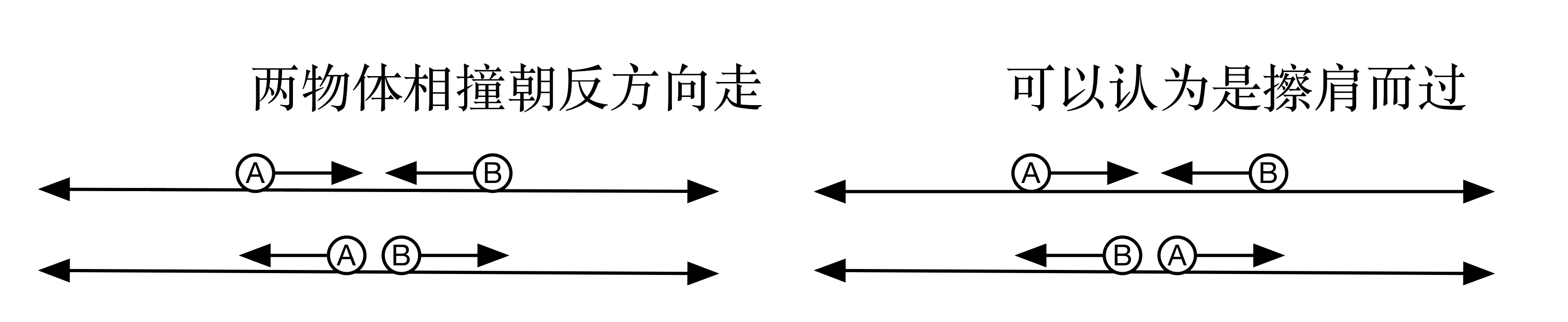
这非常好理解,如果个体之间没有差异,那么无论是擦身而过,或是相撞掉头,总的运动情况并没有改变。实际上,这是最重要的一条基本思想。
- 引理二:无论如何碰撞,刚体的顺序始终与开始时相同(即相对位置不变)

稍微思考一下,就会发现是对的。先考虑2个物体A、B,若A在左,B在右,无论怎么碰撞,A一定在左,B一定在右。
如果有三个物体A、B、C依次从左到右,同样也是成立的。推广到n个物体,也遵循相对位置不变。
推论
既然我们有了引理一、二,我们可以运用它们,避免对物理运动进行模拟,来求得每个物体在时刻 的位置。
由引理一,忽略个体的差异,那么两个刚体相撞掉头可以看作保持原样运动擦身而过。我们让每个物体按照各自的方向和速度运动 秒,这时可知,所有物体的位置(忽略个体差异)与相撞掉头的情况是一模一样的。
再由引理二,无论如何碰撞,刚体的相对位置相同,所以我们将之前的坐标排序。 时刻最左边的物体,一定对应起始时刻最左边的物体。以此类推,我们按照初始的相对位置,可以得到之前算出来的坐标上分别对应的物体。
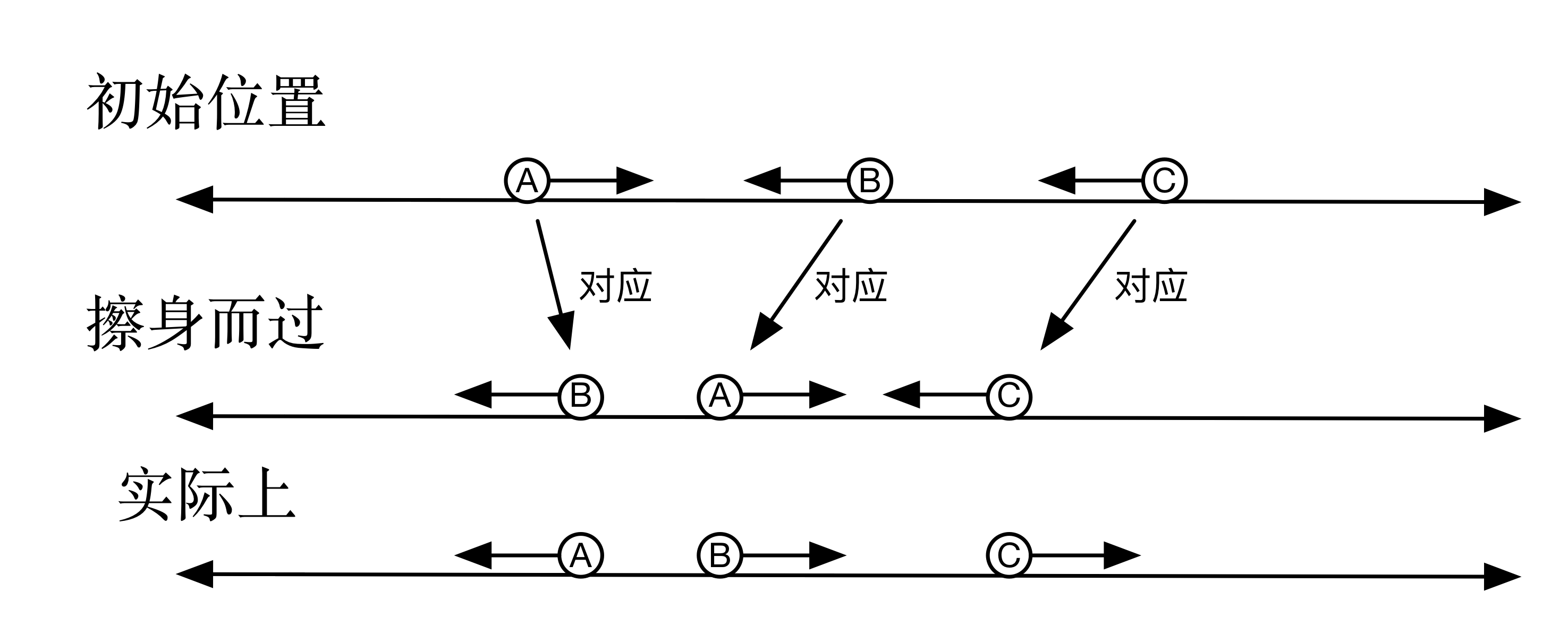
图中的对应关系,则是由引理二得到,这一对应,一定要仔细想清楚(其实也很好想对不对)。
实战
有了前面的铺垫,下面的题目都可以轻松解决了。
Ants(Poj No.1852)
n只蚂蚁以每秒1cm的速度在长为Lcm的竿子上爬行。当蚂蚁爬到竿子的端点时就会掉落。由于竿子太细,两只蚂蚁相遇时,它们不能交错通过,只能各自反向爬回去。对于每只蚂蚁,我们知道它距离竿子左端的距离xi,但不知道它当前的朝向。请计算所有蚂蚁落下竿子所需的最短时间和最长时间。
很简单,距离杆子两端最远点掉下去的时间的就是最长时间,反之最近对应最短时间。
Linear world(Poj No.2674)
在一个一维的世界里有N个居民在一条直线上的不同位置,他们以恒定的速度大小进行运动,运动方向可能不同,相遇后会各自掉头。给定线段的长度l,速度v,求最后一个走出这个范围的居民是谁,用时多少?
首先根据引理一,可求得最后一个人走出的时间(但无法确定是谁),注意走出左端右端都算走出范围。之后所有人按照自己的方向运动这个时间,现在总的运动情况与相遇掉头的情况是一样的。最后根据引理二,对应得到最后一个走出的人是谁。
