BZOJ 2132 - 圈地计划 | Sengxian's Blog

BZOJ 2132 - 圈地计划

#最大权闭合子图 #最小割 #网络流

Published on 2016-03-23

描述

最近房地产商 GDOI(Group of Dumbbells Or Idiots) 从 NOI(Nuts Old Idiots) 手中得到了一块开发土地。据了解，这块土地是一块矩形的区域，可以纵横划分为 $N\times M(N, M \le 100)$ 块小区域。GDOI 要求将这些区域分为商业区和工业区来开发。根据不同的地形环境，每块小区域建造商业区和工业区能取得不同的经济价值。更具体点，对于第 $i$ 行第 $j$ 列的区域，建造商业区将得到 $A_{i, j}$ 收益，建造工业区将得到 $B_{ij}$ 收益。另外不同的区域连在一起可以得到额外的收益，即如果区域 $(i,j)$ 相邻（相邻是指两个格子有公共边）有 $K$ 块（显然 $K$ 不超过 4）类型不同于 $(i,j)$ 的区域，则这块区域能增加 $k\times C_{i, j}$ 收益。经过 Tiger.S 教授的勘察，收益矩阵 $A,B,C$ 都已经知道了。你能帮 GDOI 求出一个收益最大的方案么？

样例输入

样例输出

分析

费用流显然不能捉，流量无法复用。那么只能转换为最小割。
由于每一个方案总的收益等于所有可能的收益－不能达到的收益。
所以我们用最小割最小化不能达到的收益，这是一个最大权闭合图的技巧。
对矩阵黑白染色，这样就变成二分图，我们以黑点为 $X$ 集，白点为 $Y$ 集，建图如下：

新建源点汇点 $s, t$ ，对于每个黑点 $i$ ，连一条边 $(s, i)$ ，流量为 $A_i$ ；连边 $(i, t)$ ，流量为 $B_i$ 。对于每个白点 $i$ ，连一条边 $(s, i)$ ，流量为 $B_i$ ；连边 $(i, t)$ ，流量为 $A_i$ 。
对于每个黑点 $i$ ，对与其相连的白点 $j$ 连一无向边 $(i, j)$ ，流量为 $C_i + C_j$ 。

这样建图的目的就是如果选择一样的，需要多割一条边来减去相邻的收益，一幅图就明白了。

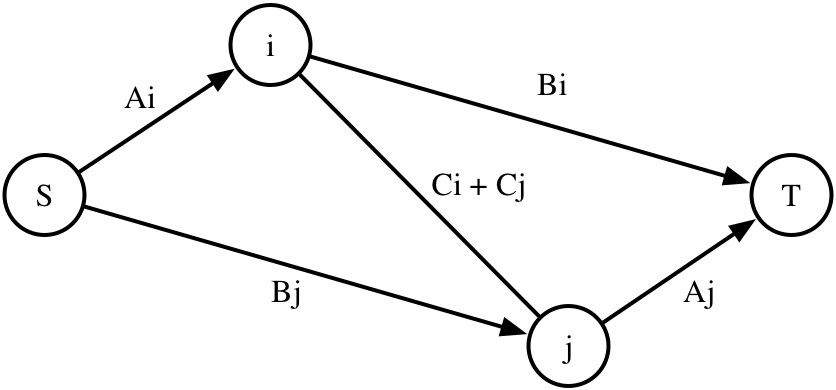
不难发现，割掉谁就代表不选谁，如果同时割 $A$ 或者 $B$ ，那么就需要割掉中间的边，因为并不能增加收益了。答案就是图中所有边的权值减去最小割。

那么，会不会出现这样一种情况呢？

已经割了两条边了，理应割 $(i, j)$ ，有没有可能 $C_i + C_j$ 太大了，割掉 $(S, i)$ 了呢？并不可能，因为这样，还不如只割 $(S, i)(S, j)$ 来的划算，所以，只要图建的合理，最小割一定是合法方案。

代码

//  Created by Sengxian on 3/23/16.
//  Copyright (c) 2016年 Sengxian. All rights reserved.
//    BZOJ 2132 网络流
#include <algorithm>
#include <iostream>
#include <cassert>
#include <cctype>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <vector>
#include <stack>
#include <queue>
using namespace std;

inline int ReadInt() {
    int n = 0, ch = getchar();
    while (!isdigit(ch)) ch = getchar();
    while (isdigit(ch)) n = (n << 3) + (n << 1) + ch - '0', ch = getchar();
    return n;
}

struct edge {
    int to, cap, rev;
    edge (int to, int cap, int rev): to(to), cap(cap), rev(rev) {}
};
const int maxn = 100 + 3, maxm = 100 + 3, INF = 0x3f3f3f3f;
struct Dinic {
    static const int maxNode = maxn * maxm + 3;
    vector<edge> G[maxNode];
    int iter[maxNode], level[maxNode], s, t;
    void addEdge(int f, int t, int cap) {
        G[f].push_back(edge(t, cap, G[t].size()));
        G[t].push_back(edge(f, 0, G[f].size() - 1));
    }
    bool Bfs() {
        memset(level, -1, sizeof level);
        queue<int> q;
        level[s] = 0, q.push(s);
        while (!q.empty()) {
            int cur = q.front(); q.pop();
            for (int i = 0; i < (int)G[cur].size(); ++i) {
                edge &e = G[cur][i];
                if (e.cap > 0 && level[e.to] == -1) {
                    level[e.to] = level[cur] + 1;
                    q.push(e.to);
                }
            }
        }
        return ~level[t];
    }
    int Dfs(int cur, int flow) {
        if (cur == t || flow == 0) return flow;
        for (int &i = iter[cur]; i < (int)G[cur].size(); ++i) {
            edge &e = G[cur][i];
            if (e.cap > 0 && level[e.to] == level[cur] + 1) {
                int d = Dfs(e.to, min(flow, e.cap));
                if (d > 0) {
                    e.cap -= d;
                    G[e.to][e.rev].cap += d;
                    return d;
                }
            }
        }
        return 0;
    }
    int maxFlow(int s, int t) {
        this -> s = s, this -> t = t;
        int flow = 0, d = 0;
        while (Bfs()) {
            memset(iter, 0, sizeof iter);
            while (d = Dfs(s, INF), d > 0) flow += d;
        }
        return flow;
    }    
}Dinic;

int n, m, c[maxn][maxm];
inline bool getColor(int x, int y) {return (x + y) & 1;}
inline int ID(int x, int y) {return x * m + y;}

int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};

int main() {
    freopen("test.in", "r", stdin);
    int sum = 0;
    n = ReadInt(), m = ReadInt();
    int s = n * m, t = n * m + 1, x;
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < m; ++j) {
            sum += x = ReadInt();
            if (getColor(i, j)) Dinic.addEdge(s, ID(i, j), x);
            else Dinic.addEdge(t, ID(i, j), x);
        }
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < m; ++j) {
            sum += x = ReadInt();
            if (!getColor(i, j)) Dinic.addEdge(s, ID(i, j), x);
            else Dinic.addEdge(t, ID(i, j), x);
        }
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < m; ++j)
            c[i][j] = ReadInt();
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < m; ++j) if (getColor(i, j))
            for (int k = 0; k < 4; ++k) {
                int x = i + dx[k], y = j + dy[k];
                if (x >= 0 && y >= 0 && x < n && y < m)
                    Dinic.addEdge(ID(i, j), ID(x, y), c[i][j] + c[x][y]),
                    sum += c[i][j] + c[x][y];
            }
    printf("%d\n", sum - Dinic.maxFlow(s, t));
    return 0;
}

非旋转 Treap 及可持久化 Treap 线性规划与网络流24题